
【题目】(1)在平面直角坐标系中A(5,0),B为y轴上任意一点,以点B为直角顶点作等腰Rt△ABC(点A、B、C按顺时针方向排列),请探究点C是否在一确定的直线上;
(2)在平面直角坐标系中,A(﹣1,0),B(4,2m),连接AB,将AB绕点B逆时针旋转90°到CB,请探究点C是否在一确定的直线上.
【答案】(1)见解析;(2)见解析.
【解析】
(1)如图1中,在y轴的正半轴上取一点D,使得OD=OA=5,证明△OAB∽△DAC,推出∠CDA=90°即可解决问题.
(2)如图2中,点B在直线x=4上,取一点D,使得DH=AH=1,证明△HAB∽△DAC,推出∠ADC=∠AHB=90°,即可解决问题.
解:(1)如图1中,在y轴的正半轴上取一点D,使得OD=OA=5,
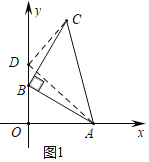
∵OD=OA,∠AOD=90°,
∴∠OAD=45°,
∵∠CAB=45°,
∴∠OAD=∠CAB,
∴∠OAB=∠DAC,
∵![]() =
=![]() =
=![]() ,
,
∴△OAB∽△DAC,
∴∠AOB=∠ADC=90°,
∴∠ODC=135°,
∴直线CD的解析式为y=x+5,
∴C是在一确定的直线上;
(2)如图2中,点B在直线x=4上,取一点D,使得DH=AH=1,
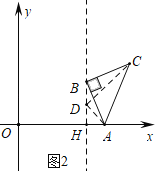
同法可证:△HAB∽△DAC,
∴∠ADC=∠AHB=90°,
∴∠CDH=135°,
∴直线CD的解析式为y=x﹣3,
∴点C在一确定的直线上.


科目:初中数学 来源: 题型:
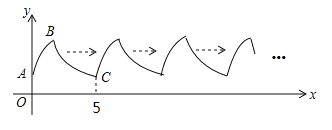
【题目】如图,曲线AB是抛物线![]() 的一部分(其中A是抛物线与y轴的交点,B是顶点),曲线BC是双曲线
的一部分(其中A是抛物线与y轴的交点,B是顶点),曲线BC是双曲线![]() 的一部分.曲线AB与BC组成图形W由点C开始不断重复图形W形成一组“波浪线”.若点
的一部分.曲线AB与BC组成图形W由点C开始不断重复图形W形成一组“波浪线”.若点![]() ,
,![]() 在该“波浪线”上,则m的值为________,n的最大值为________.
在该“波浪线”上,则m的值为________,n的最大值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,AD是∠BAC的平分线,E为AD上一点,以BE为一边且在BE下方作等边三角形BEF,连接CF.
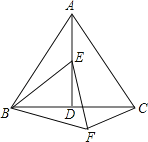
(1)求证:△ABE≌△CBF;
(2)求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先化简,再求值:(a+b)(a﹣b)+(a+b)2-2a2,其中a=﹣2﹣![]() ,b=
,b=![]() ﹣2
﹣2
(2)如图①,小红家阳台上放置了一个可折叠的晒衣架,图②是晒衣架的侧面示意图,经测量:OC=OD=126cm,OA=OB=56cm,且AB=32cm,求此时C,D两点间的距离.
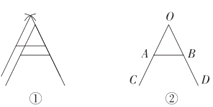
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=2x2+4x+k﹣1(k为大于2的正整数)与x轴有交点.
(1)求k的值及抛物线y=2x2+4x+k﹣1的对称轴;
(2)将抛物线y=2x2+4x+k﹣1在直线y=2上方的部分沿直线y=2翻折,其余部分不变,得到一个新图象,当直线y=![]() x+b与此图象有两个公共点时,求b的取值范围.
x+b与此图象有两个公共点时,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有若干间标准房,当标准房的价格为![]() 元时,每天入住的国间数为
元时,每天入住的国间数为![]() 间,经市场调查表明,该宾馆每间标准房的价格在
间,经市场调查表明,该宾馆每间标准房的价格在![]() 元之间(含
元之间(含![]() 元,
元,![]() 元)浮动时,每天人住的房间数
元)浮动时,每天人住的房间数![]() (间)与每间标准房的价格
(间)与每间标准房的价格![]() (元)的数据如下表:
(元)的数据如下表:
| …… | 190 | 200 | 210 | 220 | …… |
| …… | 65 | 60 | 55 | 50 | …… |
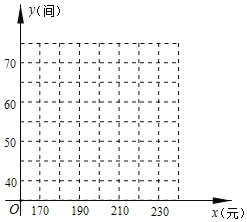
(1)根据所给数据在坐标系中描出相应的点,并画出图象.
(2)猜想(1)中的图象是什么函数的图象,求![]() 关于
关于![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围.
的取值范围.
(3)设客房的日营业额为W (元).若不考虑其他因素,问宾馆标准房的价格定为多少元时,客房的日营业额最大?最大为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,圆O是以AB为直径的△ABC的外接圆,D是劣弧![]() 的中点,连AD并延长与过C点的切线交于点P,OD与BC相交于E;
的中点,连AD并延长与过C点的切线交于点P,OD与BC相交于E;
(1)求证:OE=![]() AC;
AC;
(2)求证:![]() ;
;
(3)当AC=6,AB=10时,求切线PC的长.
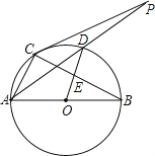
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某路灯在铅垂面内的示意图,灯柱BC的高为10米,灯柱BC与灯杆AB的夹角为120°.路灯采用锥形灯罩,在地面上的照射区域DE的长为13.3米,从D、E两处测得路灯A的仰角分别为α和45°,且tanα=6.求灯杆AB的长度.
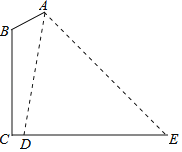
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E为BC上的点,AD平分∠BAE,CA=CD.
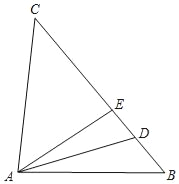
(1)求证:∠CAE=∠B;
(2)若∠B=50°,∠C=3∠DAB,求∠C的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com