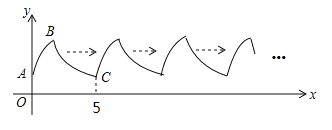
【题目】如图，曲线AB是抛物线
的一部分（其中A是抛物线与y轴的交点，B是顶点），曲线BC是双曲线
的一部分.曲线AB与BC组成图形W由点C开始不断重复图形W形成一组“波浪线”.若点
，
在该“波浪线”上，则m的值为________，n的最大值为________.
【答案】1 5
【解析】
由二次函数解析式可得点A坐标，由图象可知A、C之间的距离为5，即可判断点P与点A的纵坐标相同，由反比例函数图象可知在每个区间y随x的增大而减小，可得该“波浪线”上y的最大值为二次函数的最大值，把二次函数解析式配方成顶点式，可得函数最大值，即可得n的最大值.
∵抛物线解析式为
，
∴x=0时，y=1，
∴点A坐标为（0，1）
由图象可知A、C之间的距离为5，
∴2020÷5=404，
∴点P与点A的纵坐标相同，
∴m=1，
由反比例函数图象可知，在每个区间y随x的增大而减小，
∴该“波浪线”上y的最大值为二次函数的最大值，
∵=-4(x-1)2+5，
∴该二次函数的最大值为5，
∴n的最大值为5.
故答案为：1，5
科目：初中数学 来源： 题型：
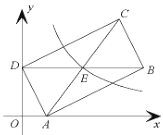
【题目】如图，在平面直角坐标系中，矩形
的顶点
，
分别在
轴、
轴上，对角线
轴，反比例函数
的图象经过矩形对角线的交点
，若点
，
，则
的值为__________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一辆慢车从甲地匀速行驶至乙地，一辆快车同时从乙地出发匀速行驶至甲地，两车之间的距离y（千米）与行驶时间x（小时）的对应关系如图所示，下列叙述正确的是（ ）
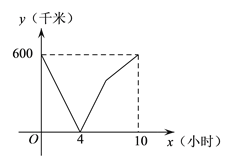
A. 甲乙两地相距1200千米
B. 快车的速度是80千米∕小时
C. 慢车的速度是60千米∕小时
D. 快车到达甲地时，慢车距离乙地100千米
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】十八大以来，某校已举办五届校园艺术节.为了弘扬中华优秀传统文化，每届艺术节上都有一些班级表演“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”等节目.小颖对每届艺术节表演这些节目的班级数进行统计，并绘制了如图所示不完整的折线统计图和扇形统计图.
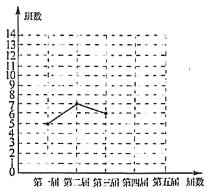
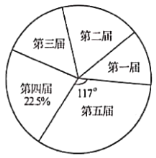
(1)五届艺术节共有________个班级表演这些节日，班数的中位数为________，在扇形统计图中，第四届班级数的扇形圆心角的度数为________；
(2)补全折线统计图；
(3)第六届艺术节，某班决定从这四项艺术形式中任选两项表演(“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”分别用
，
，
，
表示).利用树状图或表格求出该班选择和两项的概率.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某生物小组观察一植物生长，得到的植物高度y（单位：厘米）与观察时间x（单位：天）的关系，并画出如图所示的图象（AC是线段，直线CD平行于x轴）．下列说法正确的是（ ）．
①从开始观察时起，50天后该植物停止长高；
②直线AC的函数表达式为
；
③第40天，该植物的高度为14厘米；
④该植物最高为15厘米．
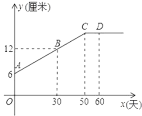
A.①②③B.②④C.②③D.①②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠C=90°，∠A=30°，BD为△ABC的角平分线，若AC= 12 ,则在△ABD中AB边上的高为（ ）
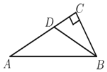
A.3B.4C.5D.6
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线y=ax2+bx-5的经过点（-2,-15）、点（2,1）．
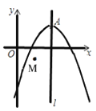
（1）求抛物线的表达式；
（2）请用配方法求抛物线顶点A的坐标；
（3）已知点M坐标为（2，—1）．设动点P、Q分别在抛物线和对称轴
上，当以A，P，Q，M为顶点的四边形是平行四边形时，求P、Q两点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】解不等式组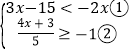
请结合题意填空，完成本题的解答．
（1）解不等式①，得________；
（2）解不等式②，得________；
（3）把不等式①和②的解集在数轴上表示出来；
（4）原不等式组的解集为___________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）在平面直角坐标系中A（5，0），B为y轴上任意一点，以点B为直角顶点作等腰Rt△ABC（点A、B、C按顺时针方向排列），请探究点C是否在一确定的直线上；
（2）在平面直角坐标系中，A（﹣1，0），B（4，2m），连接AB，将AB绕点B逆时针旋转90°到CB，请探究点C是否在一确定的直线上．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com