
【题目】解不等式组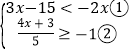
请结合题意填空,完成本题的解答.
(1)解不等式①,得________;
(2)解不等式②,得________;
(3)把不等式①和②的解集在数轴上表示出来;
![]()
(4)原不等式组的解集为___________.
科目:初中数学 来源: 题型:
【题目】阅读材料,回答问题:
两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,我们就说这两个代数式互为有理化因式.例如:因为![]() ,
,![]() ,所
,所![]() 与
与![]() ,
,![]() 与
与![]() 互为有理化因式.
互为有理化因式.
(1)![]() 的有理化因式是 ;
的有理化因式是 ;
(2)这样,化简一个分母含有二次根式的式子时,采用分子、分母同乘以分母的有理化因式的方法就可以了,例如:
![]() ,
,

用上述方法对![]() 进行分母有理化.
进行分母有理化.
(3)利用所需知识判断:若![]() ,
,![]() ,则
,则![]() 的关系是 .
的关系是 .
(4)直接写结果:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图I,在![]() 中,
中,![]() .点
.点![]() 在
在![]() 外,连接
外,连接![]() ,作
,作![]() ,交
,交![]() 于点
于点![]() ,
,![]() ,
,![]() ,连接
,连接![]() .则
.则![]() 间的等量关系是______;(不用证明)
间的等量关系是______;(不用证明)
(2)如图Ⅱ,![]() ,
,![]() ,
,![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,写出
,写出![]() 间的等量关系,并证明你的结论.
间的等量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=ax2+bx+c(a≠0)经过点A(﹣2,0)、B(4,0)、C(0,﹣8),与直线y=x﹣4交于B,D两点
(1)求抛物线的解析式并直接写出D点的坐标;
(2)点P为直线BD下方抛物线上的一个动点,试求出△BDP面积的最大值及此时点P的坐标;
(3)点Q是线段BD上异于B、D的动点,过点Q作QF⊥x轴于点F,交抛物线于点G,当△QDG为直角三角形时,直接写出点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知OA,OB是⊙O的半径,且OA⊥OB,垂足为O,P是射线OA上的一点(点A除外),直线BP交⊙O于点Q,过Q作⊙O的切线交射线OA于点E.
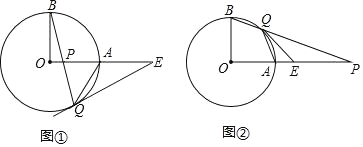
(1)如图①,点P在线段OA上,若∠OBQ=15°,求∠AQE的大小;
(2)如图②,点P在OA的延长线上,若∠OBQ=65°,求∠AQE的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系,跨度AB=44米,∠A=45°,AC1=4米,点D2的坐标为(-13,-1.69),则桥架的拱高OH=________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.

(2)结论应用:① 如图2,点M,N在反比例函数![]() (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF.
② 若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断 MN与EF是否平行?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,点E与点F分别在线段AC、BC上,且四边形DEFG是正方形.


(1)试探究线段AE与CG的关系,并说明理由.
(2)如图②若将条件中的四边形ABCD与四边形DEFG由正方形改为矩形,AB=3,BC=4.
①线段AE、CG在(1)中的关系仍然成立吗?若成立,请证明,若不成立,请写出你认为正确的关系,并说明理由.
②当△CDE为等腰三角形时,求CG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com