
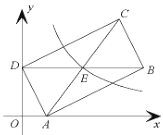
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() ,
,![]() 分别在
分别在![]() 轴、
轴、![]() 轴上,对角线
轴上,对角线![]() 轴,反比例函数
轴,反比例函数![]() 的图象经过矩形对角线的交点
的图象经过矩形对角线的交点![]() ,若点
,若点![]() ,
,![]() ,则
,则![]() 的值为__________.
的值为__________.
【答案】20
【解析】
根据平行于x轴的直线上任意两点纵坐标相同,可设B(x,4).利用矩形的性质得出E为BD中点,∠DAB=90°.根据线段中点坐标公式得出E(![]() x,4).由勾股定理得出AD2+AB2=BD2,列出方程22+42+(x-2)2+42=x2,求出x,得到E点坐标,代入y=
x,4).由勾股定理得出AD2+AB2=BD2,列出方程22+42+(x-2)2+42=x2,求出x,得到E点坐标,代入y=![]() ,利用待定系数法求出k.
,利用待定系数法求出k.
∵BD∥x轴,D(0,4),
∴B、D两点纵坐标相同,都为4,
∴可设B(x,4).
∵矩形ABCD的对角线的交点为E,
∴E为BD中点,∠DAB=90°.
∴E(![]() x,4).
x,4).
∵∠DAB=90°,
∴AD2+AB2=BD2,
∵A(2,0),D(0,4),B(x,4),
∴22+42+(x-2)2+42=x2,
解得x=10,
∴E(5,4).
∵反比例函数y=![]() (k>0,x>0)的图象经过点E,
(k>0,x>0)的图象经过点E,
∴k=5×4=20.
故答案为20.


科目:初中数学 来源: 题型:
【题目】在同一条道路上,甲车从![]() 地到
地到![]() 地,乙车从
地,乙车从![]() 地到
地到![]() 地,两车同时出发以各自速度匀速行驶. 两车相遇后,乙车休息了
地,两车同时出发以各自速度匀速行驶. 两车相遇后,乙车休息了![]() 小时,然后继续原速驶往
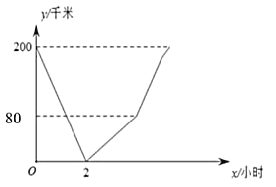
小时,然后继续原速驶往![]() 地,图中的折线段表示甲、乙两车之间的距离
地,图中的折线段表示甲、乙两车之间的距离![]() (千米)与行驶时间
(千米)与行驶时间![]() (小时)的函数关系的图象,下列说法错误的是( )
(小时)的函数关系的图象,下列说法错误的是( )
A.甲乙两车出发![]() 小时后相遇B.甲车速度是
小时后相遇B.甲车速度是![]() 千米/小时
千米/小时
C.甲车到![]() 地比乙车到
地比乙车到![]() 地早
地早![]() D.相遇时乙车距离
D.相遇时乙车距离![]() 地
地![]() 千米
千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形![]() 中,
中,![]() ,对角线
,对角线![]() 平分
平分![]() .
.
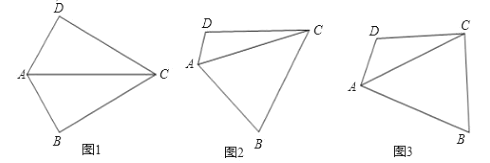
(1)如图1,若![]() ,且
,且![]() ,直接写出线段
,直接写出线段![]() 、
、![]() 、
、![]() 的数量关系.
的数量关系.
(2)如图2,若将(1)中的条件“![]() ”去掉,求边
”去掉,求边![]() 、
、![]() 与对角线
与对角线![]() 的数量关系.请证明.
的数量关系.请证明.
(3)如图3,若![]() ,直接写出边
,直接写出边![]() 、
、![]() 与对角线
与对角线![]() 的数量关系(用
的数量关系(用![]() 来表示)
来表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组在探究函数y=|x2-4x+3|的图象和性质时,经历以下几个学习过程:
(1)列表(完成以下表格)
x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y1=x2-4x+3 | … | 15 | 8 | 0 | 0 | 3 | 15 | … | |||
y=|x2-4x+3| | … | 15 | 8 | 0 | 0 | 3 | 15 | … |
(2)描点并画出函数图象草图(在备用图1中描点并画图)

(3)根据图象完成以下问题
(ⅰ)观察图象
函数y=|x2-4x+3|的图象可由函数y1=x2-4x+3的图象如何变化得到?
答:______.
(ⅱ)数学小组探究发现直线y=8与函数y=|x2-4x+3|的图象交于点E、F,E(-1,8),F(5,8),则不等式|x2-4x+3|>8的解集是______;
(ⅲ)设函数y=|x2-4x+3|的图象与x轴交于A、B两点(B位于A的右侧),与y轴交于点C.
①求直线BC的解析式;
②探究应用:将直线BC沿y轴平移m个单位后与函数y=|x2-4x+3|的图象恰好有3个交点,求此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
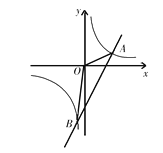
【题目】如图,直线y1=3x﹣5与反比例函数y2=![]() 的图象相交A(2,m),B(n,﹣6)两点,连接OA,OB.
的图象相交A(2,m),B(n,﹣6)两点,连接OA,OB.
(1)求k和n的值;
(2)求△AOB的面积;
(3)直接写出y1> y2时自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=![]() (k是常数).
(k是常数).
(1)若该函数的图象与x轴有两个不同的交点,试求k的取值范围;
(2)若点(1,k)在某反比例函数图象上,要使该反比例函数和二次函数y=![]() 都是y随x的增大而增大,求k应满足的条件及x的取值范围;
都是y随x的增大而增大,求k应满足的条件及x的取值范围;
(3)若抛物线y=![]() 与x轴交于A(
与x轴交于A(![]() ,0)、B(
,0)、B(![]() ,0)两点,且
,0)两点,且![]() <
<![]() ,
,![]() =34,若与y轴不平行的直线y=ax+b经过点P(1,3),且与抛物线交于
=34,若与y轴不平行的直线y=ax+b经过点P(1,3),且与抛物线交于![]() (
(![]() ,
,![]() )、
)、![]() (
(![]() ,
,![]() )两点,试探究
)两点,试探究![]() 是否为定值,并写出探究过程.
是否为定值,并写出探究过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家创新指数是反映一个国家科学技术和创新竞争力的综合指数.对国家创新指数得分排名前40的国家的有关数据进行收集、整理、描述和分析.下面给出了部分信息:
a.国家创新指数得分的频数分布直方图(数据分成7组:
30≤x<40,40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100);
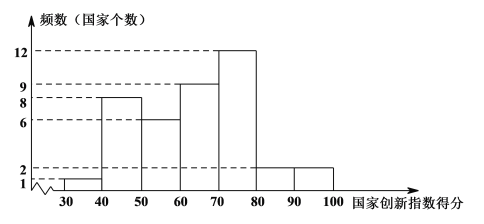
b.国家创新指数得分在60≤x<70这一组的是:61.7 62.4 63.6 65.9 66.4 68.5 69.1 69.3 69.5
c.40个国家的人均国内生产总值和国家创新指数得分情况统计图:
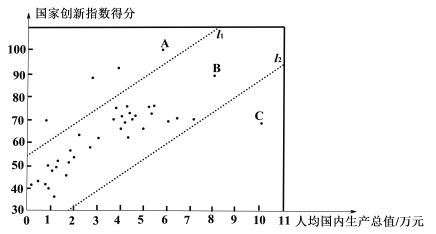
d.中国的国家创新指数得分为69.5.
(以上数据来源于《国家创新指数报告(2018)》)
根据以上信息,回答下列问题:
(1)中国的国家创新指数得分排名世界第______;
(2)在40个国家的人均国内生产总值和国家创新指数得分情况统计图中,包括中国在内的少数几个国家所对应的点位于虚线![]() 的上方.请在图中用“
的上方.请在图中用“![]() ”圈出代表中国的点;
”圈出代表中国的点;
(3)在国家创新指数得分比中国高的国家中,人均国内生产总值的最小值约为______万美元;(结果保留一位小数)
(4)下列推断合理的是______.
①相比于点A,B所代表的国家,中国的国家创新指数得分还有一定差距,中国提出“加快建设创新型国家”的战略任务,进一步提高国家综合创新能力;
②相比于点B,C所代表的国家,中国的人均国内生产总值还有一定差距,中国提出“决胜全面建成小康社会”的奋斗目标,进一步提高人均国内生产总值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形![]() ,
,![]() ,
,![]() ,
,![]() 为边
为边![]() 上任意一点,连结
上任意一点,连结![]() ,
,![]() ,以
,以![]() 为直径作
为直径作![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,连结
,连结![]() ,
,![]() .
.

(1)若点![]() 为
为![]() 的中点,证明:
的中点,证明:![]() .
.
(2)若![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的长.
的长.
(3)作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() .
.
①当点![]() 落在线段
落在线段![]() 上时,设线段
上时,设线段![]() ,
,![]() 交于点
交于点![]() ,求
,求![]() 与
与![]() 的面积之比.
的面积之比.
②在点![]() 的运动过程中,当点
的运动过程中,当点![]() 落在四边形
落在四边形![]() 内时(不包括边界),则
内时(不包括边界),则![]() 的范围是________(直接写出答案).
的范围是________(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
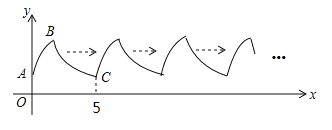
【题目】如图,曲线AB是抛物线![]() 的一部分(其中A是抛物线与y轴的交点,B是顶点),曲线BC是双曲线
的一部分(其中A是抛物线与y轴的交点,B是顶点),曲线BC是双曲线![]() 的一部分.曲线AB与BC组成图形W由点C开始不断重复图形W形成一组“波浪线”.若点
的一部分.曲线AB与BC组成图形W由点C开始不断重复图形W形成一组“波浪线”.若点![]() ,
,![]() 在该“波浪线”上,则m的值为________,n的最大值为________.
在该“波浪线”上,则m的值为________,n的最大值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com