
【题目】如图,在边长为2的菱形![]() 中,
中,![]() ,点
,点![]() 为射线
为射线![]() 上一个动点,过点
上一个动点,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() .将
.将![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 的对应点为
的对应点为![]() ,连接
,连接![]() ,
,![]() .若
.若![]() 为直角三角形时,
为直角三角形时,![]() 的长为__________.
的长为__________.
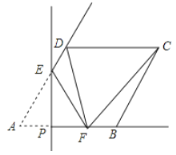
【答案】![]() 或
或![]()
【解析】
如图1,当∠CDF=90°时,根据菱形的性质得到∠AFD=∠CDF=90°,求得AF=1,由折叠的性质可得AP=![]() AF=
AF=![]() ;如图2,当∠DCF=90°,根据平行线的性质得到∠CBF=∠A=60°,根据直角三角形的性质求出BF=
;如图2,当∠DCF=90°,根据平行线的性质得到∠CBF=∠A=60°,根据直角三角形的性质求出BF=![]() BC=1,可得AF=3,由折叠的性质得到AP=
BC=1,可得AF=3,由折叠的性质得到AP=![]() AF=
AF=![]() .
.
解:如图1,当∠CDF=90°时,
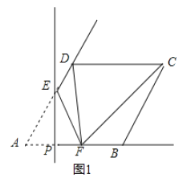
∵在菱形ABCD中,AB=CD=AD=2,CD∥AB,
∴∠AFD=∠CDF=90°,
∵∠A=60°,
∴AF=![]() AD=1,
AD=1,
由折叠的性质可得:AP=![]() AF=
AF=![]() ;
;
如图2,当∠DCF=90°,则∠AFC=90°,
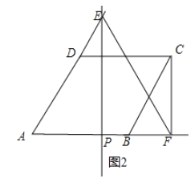
∵AD∥BC,
∴∠CBF=∠A=60°,
∵BC=2,
∴BF=![]() BC=1,
BC=1,
∴AF=3,
由折叠的性质可得:AP=![]() AF=
AF=![]() ,
,
综上所述:当△FDC为直角三角形时,AP的长为![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是边长为
是边长为![]() 的等边三角形,动点
的等边三角形,动点![]() ,
,![]() 同时从
同时从![]() ,
,![]() 两点出发,分别沿
两点出发,分别沿![]() ,
,![]() 匀速运动,其中点
匀速运动,其中点![]() 运动的速度是
运动的速度是![]() ,点
,点![]() 运动的速度是
运动的速度是![]() ,当点
,当点![]() 到达点
到达点![]() 时,
时,![]() ,
,![]() 两点都停止运动,设运动时间为
两点都停止运动,设运动时间为![]() ,解答下列问题:
,解答下列问题:
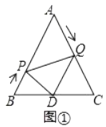
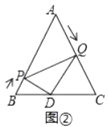
(1)如图①,当![]() 为何值时,
为何值时,![]() ;
;
(2)如图②,当![]() 为何值时,
为何值时,![]() 为直角三角形;
为直角三角形;
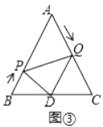
(3)如图③,作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,当
,当![]() 为何值时,
为何值时,![]() 与
与![]() 相似?
相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有若干间标准房,当标准房的价格为![]() 元时,每天入住的国间数为
元时,每天入住的国间数为![]() 间,经市场调查表明,该宾馆每间标准房的价格在
间,经市场调查表明,该宾馆每间标准房的价格在![]() 元之间(含
元之间(含![]() 元,
元,![]() 元)浮动时,每天人住的房间数
元)浮动时,每天人住的房间数![]() (间)与每间标准房的价格
(间)与每间标准房的价格![]() (元)的数据如下表:
(元)的数据如下表:
| …… | 190 | 200 | 210 | 220 | …… |
| …… | 65 | 60 | 55 | 50 | …… |
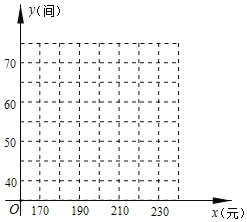
(1)根据所给数据在坐标系中描出相应的点,并画出图象.
(2)猜想(1)中的图象是什么函数的图象,求![]() 关于
关于![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围.
的取值范围.
(3)设客房的日营业额为W (元).若不考虑其他因素,问宾馆标准房的价格定为多少元时,客房的日营业额最大?最大为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
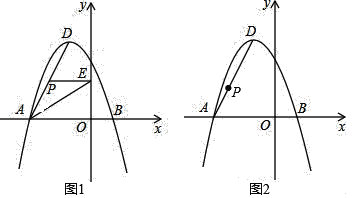
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+3经过A(﹣3,0)、B(1,0)两点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合).
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如图1,过点P作PE⊥y轴于点E.求△PAE面积S的最大值;
(3)如图2,抛物线上是否存在一点Q,使得四边形OAPQ为平行四边形?若存在求出Q点坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某路灯在铅垂面内的示意图,灯柱BC的高为10米,灯柱BC与灯杆AB的夹角为120°.路灯采用锥形灯罩,在地面上的照射区域DE的长为13.3米,从D、E两处测得路灯A的仰角分别为α和45°,且tanα=6.求灯杆AB的长度.
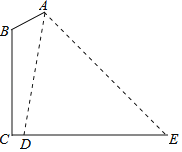
查看答案和解析>>
科目:初中数学 来源: 题型:
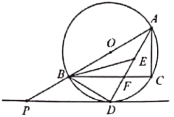
【题目】如图,![]() 内接于以
内接于以![]() 为直径的
为直径的![]() 中,且点
中,且点![]() 是
是![]() 的内心,
的内心,![]() 的延长线与
的延长线与![]() 交于点
交于点![]() ,与
,与![]() 交于点
交于点![]() ,
,![]() 的切线
的切线![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)试判断![]() 的形状,并给予证明;
的形状,并给予证明;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
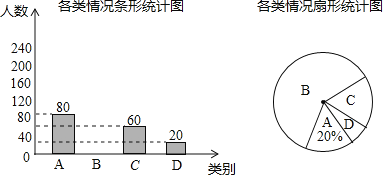
【题目】“安全教育”是学校必须开展的一项重要工作.某校为了了解家长和学生参与“暑期安全知识学习”的情况,进行了网上测试,并在本校学生中随机抽取部分学生进行调查.若把参与测试的情况分为![]() 类情形:
类情形:![]() .仅学生自己参与;
.仅学生自己参与;![]() .家长和学生一起参与;
.家长和学生一起参与;![]() .仅家长自己参与;
.仅家长自己参与;![]() .家长和学生都未参与.根据调查情况,绘制了以下不完整的统计图.请根据图中提供的信息,解答下列问题:
.家长和学生都未参与.根据调查情况,绘制了以下不完整的统计图.请根据图中提供的信息,解答下列问题:
![]() 在这次抽样调查中,共调查了 名学生;
在这次抽样调查中,共调查了 名学生;
![]() 补全条形统计图,并计算扇形统计图中
补全条形统计图,并计算扇形统计图中![]() 类所对应扇形的圆心角的度数;
类所对应扇形的圆心角的度数;
![]() 根据抽样调查结果,估计该校
根据抽样调查结果,估计该校![]() 名学生中“家长和学生都未参与”的人数.
名学生中“家长和学生都未参与”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为调查市市民上班时最常用的交通工具的情况,随机抽取了部分市民进行调查,要求被调查者从“A:自行车,B:电动车,C:公交车,D:家庭汽车,E:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题:
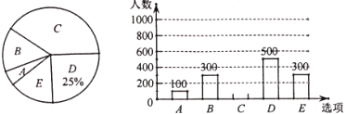
(1)在这次调查中,一共调查了 名市民,扇形统计图中,C组对应的扇形圆心角是 ;
(2)请补全条形统计图;
(3)若甲、乙两人上班时从A,B,C三种交通工具中随机选择一种,乙上班时从B、C、D三种交通工具中随机选择一种,请用树状图法或列表法求甲、乙两人都不选B种交通工具上班的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com