
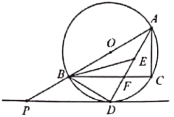
【题目】如图,![]() 内接于以
内接于以![]() 为直径的
为直径的![]() 中,且点
中,且点![]() 是
是![]() 的内心,
的内心,![]() 的延长线与
的延长线与![]() 交于点
交于点![]() ,与
,与![]() 交于点
交于点![]() ,
,![]() 的切线
的切线![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)试判断![]() 的形状,并给予证明;
的形状,并给予证明;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)![]() 是等腰直角三角形,证明见解析;(2)AE=
是等腰直角三角形,证明见解析;(2)AE=![]() .
.
【解析】
(1)根据圆周角定理的推论可得∠BDA=90°,∠ACB=90°,然后根据内心的性质结合三角形外角的性质求出∠BED=45°即可得到![]() 是等腰直角三角形;
是等腰直角三角形;
(2)根据切线的性质求出∠POD=60°,可得∠OAD=30°,然后解等腰直角三角形求出BD=DE=![]() ,进而求出AD=
,进而求出AD=![]() 即可.
即可.
解:(1)![]() 是等腰直角三角形;
是等腰直角三角形;
证明:∵AB是直径,
∴∠BDA=90°,∠ACB=90°,
∴∠CAB+∠CBA=90°,
∵点![]() 是
是![]() 的内心,
的内心,
∴AE,BE分别是∠CAB和∠CBA的角平分线,
∴∠BED=∠BAE+∠ABE=![]() ∠CAB+
∠CAB+![]() ∠CBA=
∠CBA=![]() (∠CAB+∠CBA)=45°,
(∠CAB+∠CBA)=45°,
∴![]() 是等腰直角三角形;
是等腰直角三角形;
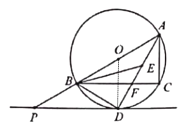
(2)连接OD,
∵![]() 是
是![]() 的切线,
的切线,
∴∠ODP=90°,
∴∠POD=90°-30°=60°,
∵OD=OA,
∴∠OAD=∠ODA=30°,
∵![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,
∴BD=DE=BE·cos45°=2×![]() ,
,
∴AD=![]() ,
,
∴AE=AD-DE=![]() .
.


科目:初中数学 来源: 题型:
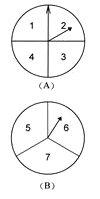
【题目】甲乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字,如图所示.游戏规定,转动两个转盘停止后,指针所指的两个数字之和为奇数时,甲获胜;为偶数时,乙获胜.
(1)用列表法(或画树状图)求甲获胜的概率;
(2)你认为这个游戏规则对双方公平吗?请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华优秀传统文化,某校组织八年级学生参加了“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,绘制如下不完整的条形统计图.
汉字听写大赛成绩分数段统计表
分数段 | 频数 |
| 2 |
| 6 |
| 9 |
| 18 |
| 15 |
汉字听写大赛成绩分数段条形统计图

(1)补全条形统计图.
(2)这次抽取的学生成绩的中位数在________的分数段中;这次抽取的学生成绩在![]() 的分数段的人数占抽取人数的百分比是_______.
的分数段的人数占抽取人数的百分比是_______.
(3)若该校八年级一共有学生350名,成绩在90分以上(含90分)为“优”,则八年级参加这次比赛的学生中成绩“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的菱形![]() 中,
中,![]() ,点
,点![]() 为射线
为射线![]() 上一个动点,过点
上一个动点,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() .将
.将![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 的对应点为
的对应点为![]() ,连接
,连接![]() ,
,![]() .若
.若![]() 为直角三角形时,
为直角三角形时,![]() 的长为__________.
的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,已知AD=10cm,tanB=2,AE⊥BC于点E,且AE=4cm,点P是BC边上一动点.若△PAD为直角三角形,则BP的长为_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织七、八、九年级学生参加“州庆60年,梦想红河”作文比赛.该校将收到的参赛作文进行分年级统计,绘制了如图1和图2两幅不完整的统计图. 根据图中提供的信息完成以下问题.
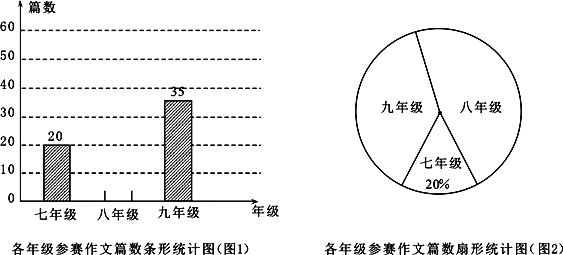
(1)扇形统计图中九年级参赛作文篇数对应的圆心角是 度,并补全条形统计图;
(2)经过评审,全校有4篇作文荣获特等奖,其中有一篇来自七年级,学校准备从特等奖作文中任选两篇刊登在校刊上,把七年级特等奖作文被选登在校刊上的事件记为A,其它年级特等奖作文被选登在校刊上的事件分别记为B,C,D. 请利用画树状图或列表的方法求出七年级特等奖作文被选登在校刊上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
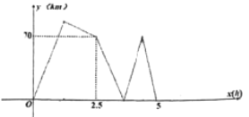
【题目】甲乙两地相距300![]() ,一辆货车和一辆轿车先后从甲地出发到乙地停止,货车先出发从甲地匀速开往乙地,货车开出一段时间后,轿车出发,匀速行驶一段时间后接到通知提速后匀速赶往乙地(提速时间不计),最后发现轿车比货车提前0.5小时到达,下图表示两车之间的距离
,一辆货车和一辆轿车先后从甲地出发到乙地停止,货车先出发从甲地匀速开往乙地,货车开出一段时间后,轿车出发,匀速行驶一段时间后接到通知提速后匀速赶往乙地(提速时间不计),最后发现轿车比货车提前0.5小时到达,下图表示两车之间的距离![]() 与货车行驶的时间
与货车行驶的时间![]() 之间的关系,则货车行驶__________小时.两车在途中相遇.
之间的关系,则货车行驶__________小时.两车在途中相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
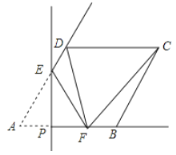
【题目】如图1,在矩形纸片![]() 中,
中,![]() ,
,![]() ,折叠纸片使
,折叠纸片使![]() 点落在边
点落在边![]() 上的
上的![]() 处,折痕为
处,折痕为![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.

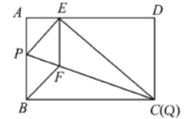
图1 图2
(1)求证:四边形![]() 为菱形;
为菱形;
(2)当点![]() 在
在![]() 边上移动时,折痕的端点
边上移动时,折痕的端点![]() ,
,![]() 也随之移动;
也随之移动;
①当点![]() 与点
与点![]() 重合时(如图2),求菱形
重合时(如图2),求菱形![]() 的边长;
的边长;
②若限定![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上移动,则点
上移动,则点![]() 在边
在边![]() 上移动的最大距离是_______.
上移动的最大距离是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com