
【题目】如图,已知![]() 是边长为
是边长为![]() 的等边三角形,动点
的等边三角形,动点![]() ,
,![]() 同时从
同时从![]() ,
,![]() 两点出发,分别沿
两点出发,分别沿![]() ,
,![]() 匀速运动,其中点
匀速运动,其中点![]() 运动的速度是
运动的速度是![]() ,点
,点![]() 运动的速度是
运动的速度是![]() ,当点
,当点![]() 到达点
到达点![]() 时,
时,![]() ,
,![]() 两点都停止运动,设运动时间为
两点都停止运动,设运动时间为![]() ,解答下列问题:
,解答下列问题:
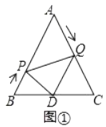
(1)如图①,当![]() 为何值时,
为何值时,![]() ;
;
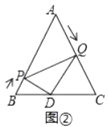
(2)如图②,当![]() 为何值时,
为何值时,![]() 为直角三角形;
为直角三角形;
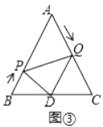
(3)如图③,作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,当
,当![]() 为何值时,
为何值时,![]() 与
与![]() 相似?
相似?
【答案】(1)![]() ;(2)3或
;(2)3或![]() ;(3)
;(3)![]() 或2
或2
【解析】
(1)先表示出AQ=2t,AP=6-t,利用AP=3AQ建立方程求解即可得出结论;
(2)分两种情况,利用含30度角的直角三角形的性质(30度角所对的直角边是斜边的一半)建立方程求解即可得出结论;
(3)先表示出BD=2t,再分两种情况:①当△BPD∽△PDQ时,判断出∠APQ=∠BDP,进而判断出△APQ∽△BDP,得出比例式建立方程求解;
②当△BPQ∽△QDP时,得出∠B=∠DQP=60°,进而判断出△APQ是等边三角形,得出AP=AQ建立方程求解即可得出结论.
(1)由题意知,![]() ,
,![]() ,
,
∵![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即:![]() 秒时,
秒时,![]() ;
;
(2)由(1)知![]() ,
,![]() ,
,![]() ,
,
∵![]() 为直角三角形,
为直角三角形,
①当![]() 时,
时,![]() ,
,
∴![]() ,∴
,∴![]() 秒,
秒,
②当![]() 时,
时,![]() ,
,
∴![]() ,
,
∴![]() 秒,
秒,
即:![]() 秒或
秒或![]() 秒时,
秒时,![]() 是直角三角形;
是直角三角形;
(3)由题意知,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∴![]() ,
,
∵![]() 与
与![]() 相似,
相似,
∴①当![]() 时,
时,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 秒,
秒,
②当![]() 时,
时,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() 秒,
秒,
即:![]() 秒或2秒时,
秒或2秒时,![]() 与
与![]() 相似.
相似.


科目:初中数学 来源: 题型:
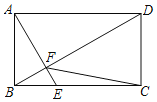
【题目】如图,在矩形ABCD中,点E是BC边上的一点,且AE⊥BD,垂足为点F,∠DAE=2∠BAE.
(1)求证:BF:DF=1:3;
(2)若四边形EFDC的面积为11,求△CEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A=30°,BD为△ABC的角平分线,若AC= 12 ,则在△ABD中AB边上的高为( )
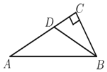
A.3B.4C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某无人机兴趣小组在操场上开展活动(如图),此时无人机在离地面30米的D处,无人机测得操控者A的俯角为37°,测得点C处的俯角为45°.又经过人工测量操控者A和教学楼BC距离为57米,求教学楼BC的高度.(注:点A,B,C,D都在同一平面上.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
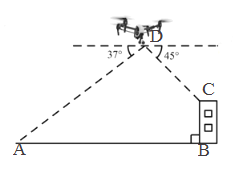
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组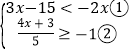
请结合题意填空,完成本题的解答.
(1)解不等式①,得________;
(2)解不等式②,得________;
(3)把不等式①和②的解集在数轴上表示出来;
![]()
(4)原不等式组的解集为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,二次函数y=![]() x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
(1)填空:b= ,c= ;
(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;
(3)点M在抛物线上,且△AOM的面积与△AOC的面积相等,求出点M的坐标。
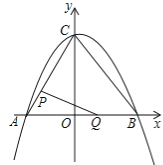
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家需要用钢管做防盗窗,按设计要求,其中需要长为 0.8m,2.5m 且粗细相同的钢管分别为 100 根,32 根,并要求这些用料不能是焊接而成的.现钢材市场的这种规格的钢管每根为 6m.
(1)试问一根 6m 长的圆钢管有哪些裁剪方法呢?请填写下空(余料作废).
方法①:当只裁剪长为 0.8m 的用料时,最多可剪 根;
方法②:当先剪下 1 根 2.5m 的用料时,余下部分最多能剪 0.8m 长的用料 根;
方法③:当先剪下 2 根 2.5m 的用料时,余下部分最多能剪 0.8m 长的用料 根.
(2)分别用(1)中的方法②和方法③各裁剪多少根 6m 长的钢管,才能刚好得到所需要的相应数量的材料?
(3)试探究:除(2)中方案外,在(1)中还有哪两种方法联合,所需要 6m 长的钢管与(2) 中根数相同?
查看答案和解析>>
科目:初中数学 来源: 题型:
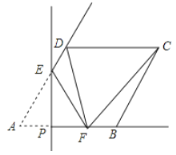
【题目】如图,在边长为2的菱形![]() 中,
中,![]() ,点
,点![]() 为射线
为射线![]() 上一个动点,过点
上一个动点,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() .将
.将![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 的对应点为
的对应点为![]() ,连接
,连接![]() ,
,![]() .若
.若![]() 为直角三角形时,
为直角三角形时,![]() 的长为__________.
的长为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com