
【题目】如图在等腰Rt△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于D,DE⊥AB于E,若AB=10,则△BDE的周长等于 . 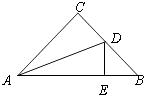
【答案】10
【解析】解:∵AD平分∠CAB,AC⊥BC于点C,DE⊥AB于E,∴CD=DE. 又∵AD=AD,
∴Rt△ACD≌Rt△AED,∴AC=AE.
又∵AC=BC,
∴BC=AE,
∴△DBE的周长为DE+BD+EB=CD+BD+EB=BC+EB=AC+EB=AE+EB=AB=10.
(提示:设法将DE+BD+EB转成线段AB).
所以答案是:10.
【考点精析】本题主要考查了等腰直角三角形和角平分线的性质定理的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,AB与CD相交于点O,∠A=∠AOC,∠B=∠BOD.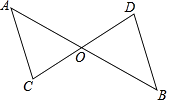
求证:∠C=∠D.
证明:∵∠A=∠AOC,∠B=∠BOD(已知)
又∠AOC=∠BOD()
∴∠A=∠B()
∴AC∥BD()
∴∠C=∠D()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,对角线AC=12,BD=8,交点为点O,则边AB的取值范围为( )
A.1<AB<2
B.2<AB<10
C.4<AB<10
D.4<AB<20
查看答案和解析>>
科目:初中数学 来源: 题型:
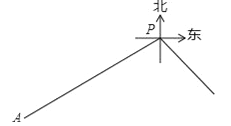
【题目】如图,甲船在港口P的南偏西60°方向,距港口86海里的A处,沿AP方向以每小时15海里的速度匀速驶向港口P.乙船从港口P出发,沿南偏东45°方向匀速驶离港口PC=2x,现两船同时出发,2小时后乙船在甲船的正东方向.求乙船的航行速度.(结果精确到个位,参考数据:![]() ,
,![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.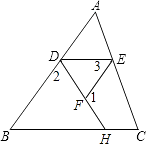
解:∵∠1+∠EFD=180°(邻补角定义),∠1+∠2=180°(已知)
∴(同角的补角相等)①
∴(内错角相等,两直线平行)②
∴∠ADE=∠3()③
∵∠3=∠B()④
∴(等量代换)⑤
∴DE∥BC()⑥
∴∠AED=∠C()⑦
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com