
【题目】在菱形ABCD中,∠A=60°,AB=4 ![]() ,点P在对角线AC上,且PB=PD=4,则∠PDC的度数为 .
,点P在对角线AC上,且PB=PD=4,则∠PDC的度数为 .
【答案】30°或90°
【解析】连接BD交AC于E,
如图,当P在对角线BD的右侧时,
在菱形ABCD中,AB=AC,BE=DE,∠BAD=60°,AB=4![]() ,
,
则△ABD是等边三角形,
则BD⊥AC,BD=AB=4![]() , BE=DE=2
, BE=DE=2![]() ,
,
则PE=![]() .
.
又因为CE=PE=![]()
则PC=PD=4,
则∠PDC=∠ACD=![]() ∠BCD=30°;
∠BCD=30°;
如图,当P在对角线BD的左侧时,
同理PD=PA,
则∠PDA=30°,
又∠CDA=180°-60°=120°,
则∠PDC=∠CDA-∠PDA=90°.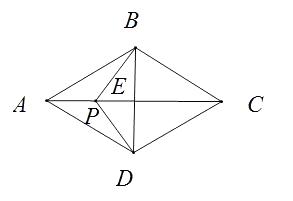
所以答案是30°或90°.
【考点精析】认真审题,首先需要了解菱形的性质(菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半).


科目:初中数学 来源: 题型:
【题目】下列各因式分解正确的是( )
A.﹣x2+(﹣2)2=(x﹣2)(x+2)
B.x2+2x﹣1=(x﹣1)2
C.4x2﹣4x+1=(2x﹣1)2
D.x2﹣4x=x(x+2)(x﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
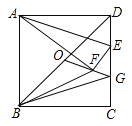
【题目】如图,在正方形ABCD中,AB=6,点E在边CD上,DE=![]() DC,连接AE,将△ADE沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长OF交CD于点G,连接BF,BG,则△BFG的周长是 .
DC,连接AE,将△ADE沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长OF交CD于点G,连接BF,BG,则△BFG的周长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式,属于二元一次方程的个数有( )
①xy+2x﹣y=7;②4x+1=x﹣y;③ ![]() +y=5;④x=y;⑤x2﹣y2=2
+y=5;④x=y;⑤x2﹣y2=2
⑥6x﹣2y ⑦x+y+z=1 ⑧y(y﹣1)=2y2﹣y2+x.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
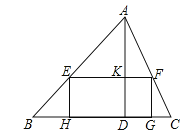
【题目】已知锐角△ABC中,边BC长为12,高AD长为8.
(1)如图,矩形EFGH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K.
①求![]() 的值;
的值;
②设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值;
(2)若AB=AC,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,直接写出正方形PQMN的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com