
【题目】已知锐角△ABC中,边BC长为12,高AD长为8.
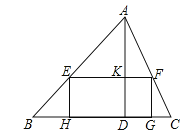
(1)如图,矩形EFGH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K.
①求![]() 的值;
的值;
②设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值;
(2)若AB=AC,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,直接写出正方形PQMN的边长.
【答案】(1)①![]() ;②
;②![]() , S的最大值是24;(2)
, S的最大值是24;(2)![]() 或
或![]() .
.
【解析】
试题分析:(1)①由EF∥BC,可得![]() ,所以
,所以![]() ,据此求出
,据此求出![]() 的值即可.
的值即可.
②由EH=x,求出AK=8﹣x,再由![]() =
=![]() ,求出EF的值;然后根据矩形的面积公式,求出S与x的函数关系式,利用配方法,求出S的最大值是多少即可.
,求出EF的值;然后根据矩形的面积公式,求出S与x的函数关系式,利用配方法,求出S的最大值是多少即可.
(2)根据题意,设正方形的边长为a,分两种情况:①当正方形PQMN的两个顶点在BC边上时;②当正方形PQMN的两个顶点在AB或AC边上时;分类讨论,求出正方形PQMN的边长各是多少即可.
试题解析:(1)①∵EF∥BC,∴![]() ,∴
,∴![]() =
=![]() =
=![]() ,即
,即![]() 的值是
的值是![]() ;
;
②∵EH=x,∴KD=EH=x,AK=8﹣x,∵![]() =
=![]() ,∴EF=
,∴EF=![]() ,∴S=EHEF=
,∴S=EHEF=![]() ,即
,即![]() ,∴当x=4时,S的最大值是24;
,∴当x=4时,S的最大值是24;
(2)设正方形的边长为a,①当正方形PQMN的两个顶点在BC边上时,![]() ,解得a=
,解得a=![]() ;
;
②当正方形PQMN的两个顶点在AB或AC边上时,∵AB=AC,AD⊥BC,∴BD=CD=12÷2=6,∴AB=AC=![]() =
=![]() =10,∴AB或AC边上的高等于:ADBC÷AB=8×12÷10=
=10,∴AB或AC边上的高等于:ADBC÷AB=8×12÷10=![]() ,∴
,∴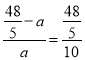 ,解得a=
,解得a=![]() ;
;
综上,可得正方形PQMN的边长是![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】△ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1:2,已知△ABC的面积是3,则△A′B′C′的面积是( )
A.3
B.6
C.9
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条城际铁路从A市到B市需要经过C市,A市位于C市西南方向,与C市相距40在千米,B市恰好位于A市的正东方向和C市的南偏东60°方向处.因打造城市经济新格局需要,将从A市到B市之间铺设一条笔直的铁路,求新铺设的铁路AB的长度.(结果保留根号)
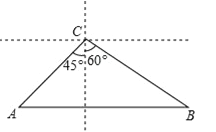
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查市场上某品牌方便面的色素含量是否符合国家标准,工作人员在超市里随机抽取了某品牌的方便面进行检验.图1和图2是根据调查结果绘制的两幅不完整的统计图,其中A、B、C、D分别代表色素含量为0.05%以下、0.05%~0.1%、0.1%~0.15%、0.15%以上,图1的条形图表示的是抽查的方便面中色素含量分布的袋数,图2的扇形图表示的是抽查的方便面中色素的各种含量占抽查总数的百分比.请解答以下问题: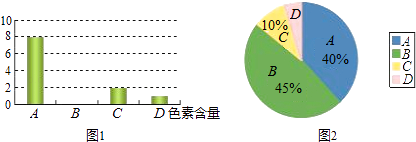
(1)本次调查一共抽查了多少袋方便面?
(2)将图1中色素含量为B的部分补充完整;
(3)图2中的色素含量为D的方便面所占的百分比是多少?
(4)若色素含量超过0.15%即为不合格产品,某超市这种品牌的方便面共有10000袋,那么其中不合格的产品有多少袋?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB与CD相交于点O,∠A=∠AOC,∠B=∠BOD.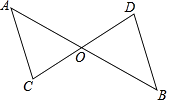
求证:∠C=∠D.
证明:∵∠A=∠AOC,∠B=∠BOD(已知)
又∠AOC=∠BOD()
∴∠A=∠B()
∴AC∥BD()
∴∠C=∠D()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.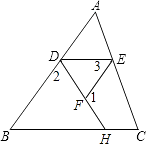
解:∵∠1+∠EFD=180°(邻补角定义),∠1+∠2=180°(已知)
∴(同角的补角相等)①
∴(内错角相等,两直线平行)②
∴∠ADE=∠3()③
∵∠3=∠B()④
∴(等量代换)⑤
∴DE∥BC()⑥
∴∠AED=∠C()⑦
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com