
【题目】完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.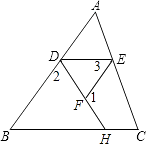
解:∵∠1+∠EFD=180°(邻补角定义),∠1+∠2=180°(已知)
∴(同角的补角相等)①
∴(内错角相等,两直线平行)②
∴∠ADE=∠3()③
∵∠3=∠B()④
∴(等量代换)⑤
∴DE∥BC()⑥
∴∠AED=∠C()⑦
【答案】∠EFD=∠2;AB∥EF;两直线平行,内错角相等;已知;∠ADE=∠B;同位角相等,两直线平行;两直线平行,同位角相等
【解析】∵∠1+∠EFD=180°(邻补角定义),∠1+∠2=180°(已知 )
∴∠EFD=∠2(同角的补角相等)①
∴AB∥EF(内错角相等,两直线平行)②
∴∠ADE=∠3(两直线平行,内错角相等)③
∵∠3=∠B(已知)④
∴∠ADE=∠B(等量代换)⑤
∴DE∥BC(同位角相等,两直线平行)⑥
∴∠AED=∠C(两直线平行,同位角相等)⑦.
答案为:∠EFD=∠2;AB∥EF;两直线平行,内错角相等;
∠ADE=∠B,同位角相等,两直线平;
两直线平行,同位角相等.
【考点精析】关于本题考查的余角和补角的特征和平行线的判定与性质,需要了解互余、互补是指两个角的数量关系,与两个角的位置无关;由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能得出正确答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
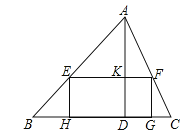
【题目】已知锐角△ABC中,边BC长为12,高AD长为8.
(1)如图,矩形EFGH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K.
①求![]() 的值;
的值;
②设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值;
(2)若AB=AC,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,直接写出正方形PQMN的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠C=90°,AE是△ABC的角平分线;ED平分∠AEB,交AB于点D;∠CAE=∠B. 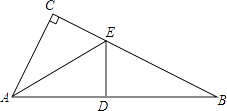
(1)求∠B的度数.
(2)如果AC=3cm,求AB的长度.
(3)猜想:ED与AB的位置关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰三角形ABC中,AB=AC=4,BC=7.如图2,在底边BC上取一点D,连结AD,使得∠DAC=∠ACD.如图3,将△ACD沿着AD所在直线折叠,使得点C落在点E处,连结BE,得到四边形ABED.则BE的长是( )
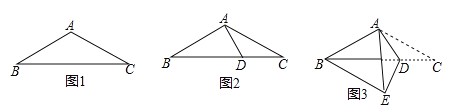
A.4 B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的个数有( )
①﹣0.5x2y3与5y2x3是同类项;
②2π与﹣4不是同类项;
③两个单项式的和一定是多项式;
④单项式mn3的系数与次数之和为4.
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD、CE是腰AB、AC上的高,交于点O. 
(1)求证:OB=OC.
(2)若∠ABC=65°,求∠COD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com