
【题目】如图,在△ABC中,AB=AC,BD、CE是腰AB、AC上的高,交于点O. 
(1)求证:OB=OC.
(2)若∠ABC=65°,求∠COD的度数.
【答案】
(1)证明:∵AB=AC,
∴∠ABC=∠ACB,
∵BD、CE是△ABC的两条高线,
∴∠BEC=∠BDC=90°,
在△BEC和△CDB中,
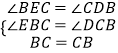 ,
,
∴△BEC≌△CDB,
∴∠DBC=∠ECB,BE=CD,
在△BOE和△COD中,
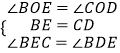 ,
,
∴△BOE≌△COD,
∴OB=OC
(2)解:∵∠ABC=65°,AB=AC,
∴∠A=180°﹣2×65°=50°,
∴∠COD=∠A=50°
【解析】(1)首先根据等腰三角形的性质得到∠ABC=∠ACB,然后利用高线的定义得到∠ECB=∠DBC,从而得证;(2)首先求出∠A的度数,进而求出∠COD的度数.
【考点精析】本题主要考查了等腰三角形的性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,AB与CD相交于点O,∠A=∠AOC,∠B=∠BOD.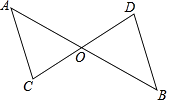
求证:∠C=∠D.
证明:∵∠A=∠AOC,∠B=∠BOD(已知)
又∠AOC=∠BOD()
∴∠A=∠B()
∴AC∥BD()
∴∠C=∠D()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.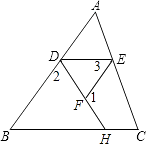
解:∵∠1+∠EFD=180°(邻补角定义),∠1+∠2=180°(已知)
∴(同角的补角相等)①
∴(内错角相等,两直线平行)②
∴∠ADE=∠3()③
∵∠3=∠B()④
∴(等量代换)⑤
∴DE∥BC()⑥
∴∠AED=∠C()⑦
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若直线l外一点P与直线l上三点的连线段长分别为2cm,3cm,4cm,则点P到直线l的距离是( )
A. 2cm B. 不超过2cm C. 3cm D. 大于4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A. 选①② B. 选选①③ C. 选②③ D. 选②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句中,正确的是
A.同一平面上三点确定一个圆
B.菱形的四个顶点在同一个圆上
C.三角形的外心是三角形三边垂直平分线的交点
D.三角形的外心到三角形三边的距离相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在所给正方形网格图中完成下列各题:(用直尺画图,保留痕迹)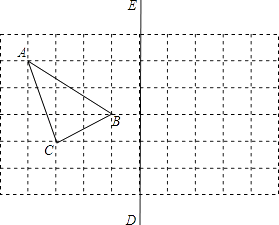
(1)求出格点△ABC(顶点均在格点上)的面积;
(2)画出格点△ABC关于直线DE对称的△A1B1C1;
(3)在DE上画出点Q,使△QAB的周长最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com