练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知同一平面上的两个角的两条边分别平行，则这两个角（ ）

    A. 相等 B. 互补 C. 相等或互补 D. 不能确定

    【答案】C

    【解析】

    一个角的两边与另一个角的两边分别平行，那么这两个角相等或互补，故答案为C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，平行四边形ABCD的顶点A，B，D的坐标分别是（0，0）、（5，0）、（2，3），则顶点C的坐标是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，BD、CE是腰AB、AC上的高，交于点O．
    （1）求证：OB=OC．
    （2）若∠ABC=65°，求∠COD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法正确的是（ ）
    A.对角线相等的平行四边形是菱形
    B.有一组邻边相等的平行四边形是菱形
    C.对角线相互垂直的四边形是菱形
    D.有一个角是直角的平行四边形是菱形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：﹣22+3×（﹣1）4﹣（﹣4）×2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，某温室屋顶结构外框为△ABC，立柱AD垂直平分横梁BC，∠B=30°，斜梁AC=4m，为增大向阳面的面积，将立柱AD增高并改变位置后变为EF，使屋顶结构外框由△ABC变为△EBC（点E在BA的延长线上）如图2所示，且立柱EF⊥BC，若EF=3m，则斜梁增加部分AE的长为m．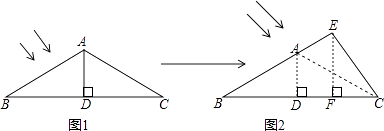

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“种瓜得瓜，种豆得豆”这一事件是 （填“必然事件”“不可能事件”“随机事件”）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面的解题过程： 已知 = ，求 的值．
    解：由 = 知x≠0，所以 =2，即x+ =2．
    ∴ =x2+ =（x+ ）2﹣2=22﹣2=2，故 的值为
    评注：该题的解法叫做“倒数法”，请你利用“倒数法”解下面的题目：
    已知 = ，求 的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题提出：
    （1）如图1，在正方形ABCD中，M是BC边（不含端点B、C）上任意一点，P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN=90°，求证：AM=MN． 下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．
    证明：在边AB上截取AE=MC，连接ME．正方形ABCD中，∠B=∠BCD=90°，AB=BC．
    ∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB=∠MAE，即∠NMC=∠MAE．
    （下面请你完成余下的证明过程）
    （2）若将（1）中的“正方形ABCD”改为“正三角形ABC”（如图2），N是∠ACP的平分线上一点，则∠AMN=60°时，结论AM=MN是否还成立？请说明理由．
    （3）若将（1）中的“正方形ABCD”改为“正n边形ABCD…X，请你作出猜想：当∠AMN=时，结论AM=MN仍然成立．（直接写出答案，不需要证明）

    查看答案和解析>>

    同步练习册答案