
【题目】问题提出: 
(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN. 下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连接ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB=∠MAE,即∠NMC=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正n边形ABCD…X,请你作出猜想:当∠AMN=时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
【答案】
(1)解:证明:如图1,

在边AB上截取AE=MC,连接ME.
∵正方形ABCD中,∠B=∠BCD=90°,AB=BC,
∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB=∠MAE,BE=AB﹣AE=BC﹣MC=BM,
∴∠BEM=45°,
∴∠AEM=135°,
∵N是∠DCP的平分线上一点,
∴∠NCP=45°,
∴∠MCN=135°,
在△AEM与△MCN中,
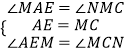 ,
,
∴△AEM≌△MCN(ASA),
∴AM=MN
(2)解:结论AM=MN还成立,
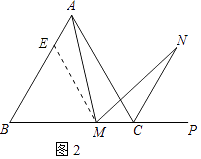
证明:如图2,在边AB上截取AE=MC,连接ME.
在正△ABC中,∠B=∠BCA=60°,AB=BC,
∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAE,BE=AB﹣AE=BC﹣MC=BM,
∴∠BEM=60°,
∴∠AEM=120°,
∵N是∠ACP的平分线上一点,
∴∠ACN=60°,
∴∠MCN=120°,
在△AEM与△MCN中,
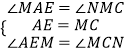 ,
,
∴△AEM≌△MCN(ASA),
∴AM=MN
(3)![]()
【解析】解决问题:(3)解:∵当AM=MN时,△AEM≌△MCN, 此时∠NMC=∠MAE,
又∵∠AMN=180°﹣∠NMC﹣∠AMB,∠MAE=180°﹣∠BAM﹣∠AMB,
∴∠AMN=∠B= ![]() ,
,
∴将(1)中的“正方形ABCD”改为“正n边形ABCD…X,则
当∠AMN= ![]() 时,结论AM=MN仍然成立.
时,结论AM=MN仍然成立.
所以答案是: ![]()
【考点精析】认真审题,首先需要了解等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°),还要掌握正方形的性质(正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形)的相关知识才是答题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在所给正方形网格图中完成下列各题:(用直尺画图,保留痕迹)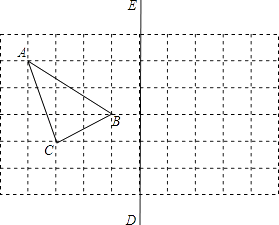
(1)求出格点△ABC(顶点均在格点上)的面积;
(2)画出格点△ABC关于直线DE对称的△A1B1C1;
(3)在DE上画出点Q,使△QAB的周长最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
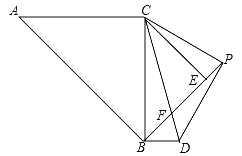
【题目】如图,△ABC和△BEC均为等腰直角三角形,且∠ACB=∠BEC=90°,AC=![]() ,点P为线段BE延长线上一点,连接CP以CP为直角边向下作等腰直角△CPD,线段BE与CD相交于点F
,点P为线段BE延长线上一点,连接CP以CP为直角边向下作等腰直角△CPD,线段BE与CD相交于点F
(1)求证:![]() ;
;
(2)连接BD,请你判断AC与BD有什么位置关系?并说明理由;
(3)设PE=x,△PBD的面积为S,求S与x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD,AE分别是△ABC的高和角平分线. 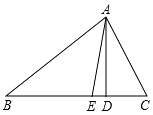
(1)已知∠B=40°,∠C=60°,求∠DAE的度数;
(2)设∠B=α,∠C=β(α<β).请用含α、β的代数式表示∠DAE.∠DAE= . 并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OD是∠AOB的角平分线,C点OD上一点.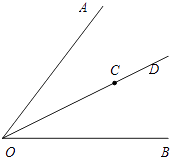
⑴过点C画直线CE∥OB,交OA于E;
⑵过点C画直线CF∥OA,交OB于F;
⑶过点C画线段CG⊥OA,垂足为G.
根据画图回答问题:
①线段长就是点C到OA的距离;
②比较大小:CECG(填“>”或“=”或“<”);
③通过度量比较∠AOD与∠ECO的关系是:∠AOD∠ECO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地之间的距离为900km,一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.已知快车的速度是慢车的2倍,慢车12小时到达甲地.
(1)慢车速度为每小时km;快车的速度为每小时km;
(2)当两车相距300km时,两车行驶了小时;
(3)若慢车出发3小时后,第二列快车从乙地出发驶往甲地,速度与第一列快车相同.在第二列快车行驶的过程中,当它和慢车相距150km时,求两列快车之间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com