
【题目】如图,AD,AE分别是△ABC的高和角平分线. 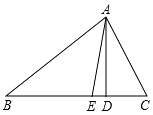
(1)已知∠B=40°,∠C=60°,求∠DAE的度数;
(2)设∠B=α,∠C=β(α<β).请用含α、β的代数式表示∠DAE.∠DAE= . 并证明.
【答案】
(1)解:∵∠B=40°,∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣40°﹣60°=80°,
∵AE是角平分线,
∴∠BAE= ![]() ∠BAC=
∠BAC= ![]() ×80°=40°,
×80°=40°,
∵AD是高,
∴∠BAD=90°﹣∠B=90°﹣40°=50°,
∴∠DAE=∠BAD﹣∠BAE=50°﹣40°=10°
(2)![]() (β﹣α)
(β﹣α)
【解析】解: (2) ![]() (β﹣α). ∵∠B=α,∠C=β(α<β),
(β﹣α). ∵∠B=α,∠C=β(α<β),
∴∠BAC=180°﹣(α+β),
∵AE是角平分线,
∴∠BAE= ![]() ∠BAC=90°﹣
∠BAC=90°﹣ ![]() (α+β),
(α+β),
∵AD是高,
∴∠BAD=90°﹣∠B=90°﹣α,
∴∠DAE=∠BAD﹣∠BAE=90°﹣α﹣[90°﹣ ![]() (α+β)]=
(α+β)]= ![]() (β﹣α).
(β﹣α).
所以答案是: ![]() (β﹣α).
(β﹣α).
【考点精析】通过灵活运用三角形的内角和外角,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角即可以解答此题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(k+1)x2+2x﹣1=0有实数根,则k的取值范围是( )
A.k≥﹣2B.k≥﹣2且k≠﹣1C.k≥2D.k≤﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=﹣x+3与x轴交于点C,与直线AD交于点A(![]() ,
,![]() ),点D的坐标为(0,1)
),点D的坐标为(0,1)
(1)求直线AD的解析式;
(2)直线AD与x轴交于点B,若点E是直线AD上一动点(不与点B重合),当△BOD与△BCE相似时,求点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出: 
(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN. 下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连接ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB=∠MAE,即∠NMC=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正n边形ABCD…X,请你作出猜想:当∠AMN=时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)

根据图表提供的信息,下列结论错误的是( )

A.这次被调查的学生人数为400人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中喜欢选修课E、F的人数分别为80,70
D.喜欢选修课C的人数最少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“立德树人,志愿服务”活动月中,学校团委为了解本校学生一个月内参加志愿服务次数的情况,随机抽取了部分同学进行统计,并将统计结果分别分成A、B、C、D四类,根据统计结果绘制了如图所示的两幅不完整的统计图.
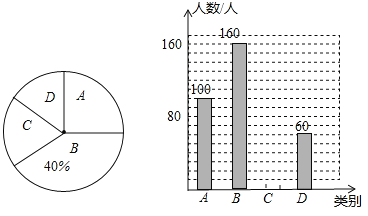
请根据图中信息解答下列问题:
(1)本次抽样调查了 名学生,并请补全条形统计图;
(2)被调查学生“一个月内参加志愿服务次数”的人数的众数落在 类.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列5个命题:①经过三个点一定可以作圆.②等弧所对的圆周角相等.③相等的圆心角所对的弦相等.④任意一个三角形一定只有一个外接圆.其中真命题有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com