
【题目】如图,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0)、(5,0)、(2,3),则顶点C的坐标是 . 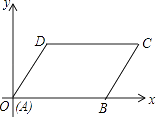
【答案】(7,3)
【解析】解:过点D作DE⊥OB于点E,过点C作CF⊥OB于点F,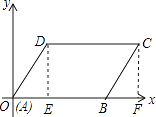
∴∠OED=∠BFC=90°,
∵平行四边形ABCD的顶点A,B,D的坐标分别是(0,0)、(5,0)、(2,3),
∴OB∥CD,OD∥BC,
∴DE=CF=3,∠DOE=∠CBF,
在△ODE和△CBF中,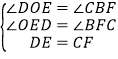 ,
,
∴△ODE≌△CBF(AAS),
∴BF=OE=2,
∴OF=OB+BF=7,
∴点C的坐标为:(7,3).
所以答案是:(7,3).
【考点精析】根据题目的已知条件,利用平行四边形的性质的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】△ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1:2,已知△ABC的面积是3,则△A′B′C′的面积是( )
A.3
B.6
C.9
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB与CD相交于点O,∠A=∠AOC,∠B=∠BOD.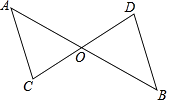
求证:∠C=∠D.
证明:∵∠A=∠AOC,∠B=∠BOD(已知)
又∠AOC=∠BOD()
∴∠A=∠B()
∴AC∥BD()
∴∠C=∠D()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,对角线AC=12,BD=8,交点为点O,则边AB的取值范围为( )
A.1<AB<2
B.2<AB<10
C.4<AB<10
D.4<AB<20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲船在港口P的南偏西60°方向,距港口86海里的A处,沿AP方向以每小时15海里的速度匀速驶向港口P.乙船从港口P出发,沿南偏东45°方向匀速驶离港口PC=2x,现两船同时出发,2小时后乙船在甲船的正东方向.求乙船的航行速度.(结果精确到个位,参考数据:![]() ,
,![]() ,
, ![]() )
)
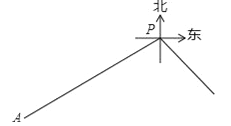
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.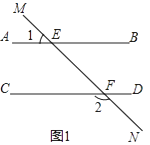
(1)试判断直线AB与CD的位置关系,并说明理由;
(2)如图2,∠AEF与∠EFC的角平分线交于点P,PF∥GH,求证:GH⊥EG;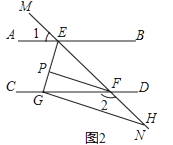
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.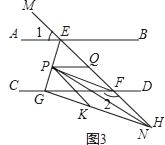
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.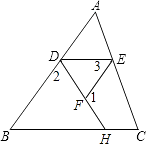
解:∵∠1+∠EFD=180°(邻补角定义),∠1+∠2=180°(已知)
∴(同角的补角相等)①
∴(内错角相等,两直线平行)②
∴∠ADE=∠3()③
∵∠3=∠B()④
∴(等量代换)⑤
∴DE∥BC()⑥
∴∠AED=∠C()⑦
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若直线l外一点P与直线l上三点的连线段长分别为2cm,3cm,4cm,则点P到直线l的距离是( )
A. 2cm B. 不超过2cm C. 3cm D. 大于4cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com