
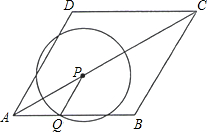
 如图,菱形ABCD的边长为2cm,∠DAB=60°.点P从A点出发,以$\sqrt{3}$cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动.设点P运动的时间为ts.
如图,菱形ABCD的边长为2cm,∠DAB=60°.点P从A点出发,以$\sqrt{3}$cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动.设点P运动的时间为ts.分析 (1)连接BD交AC于点E,由菱形的性质可知△AEB为直角三角形且∠EAB=30°,依据特殊锐角三角函数值可求得AE的长,从而得到AC的长;
(2)依据两边对应成比例且夹角相等的两三角形相似证明△APQ∽△ACB,从而得到∠APQ=∠ACB=30°;
(3)①当圆P与BC相切时,⊙P与边BC只有1个公共点,②当圆P与BC相交时,先求得圆P经过点B和点C时的t的取值,从而可确定出t的取值范围.
解答 解:(1)连接BD交AC于点E.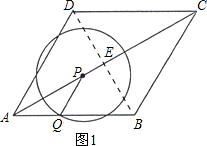
∵ABCD为菱形,∠DAB=60°,
∴∠EAB=30°,∠AEB=90°,AE=CE.
∴AE=AB×$\frac{\sqrt{3}}{2}$=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
∴AC=2$\sqrt{3}$.
(2)∵由题意可知AP=$\sqrt{3}$t,AQ=t,
∴$\frac{AP}{AQ}$=$\frac{\sqrt{3}t}{t}$=$\sqrt{3}$.
又∵$\frac{AC}{AB}=\frac{2\sqrt{3}}{2}$=$\sqrt{3}$,
∴$\frac{AP}{AQ}=\frac{AC}{AB}$.
又∵∠PAQ=∠CAB,
∴△APQ∽△ACB.
∴∠APQ=∠ACB=$\frac{1}{2}$∠DCB=30°.
(3)如图2所示:当圆P与BC相切时.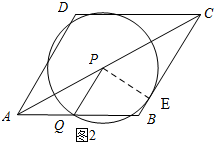
∵∠PAQ=∠APQ=30°,
∴PQ=AQ.
又∵PQ=PE,
∴AQ=PE.
∵BC为圆P的切线,
∴∠PEC=90°.
∵在△PEC中,∠PEC=90°,∠PCE=30°,
∴PC=2PE=2AQ=2t.
∵AP+PC=2$\sqrt{3}$,AP=$\sqrt{3}$t,
∴$\sqrt{3}t$+2t=2$\sqrt{3}$.
∴t=4$\sqrt{3}$-6.
∴当t=4$\sqrt{3}$-6时,圆P与BC只有一个交点.
如图3所示:当圆P经过点B时,连接PB.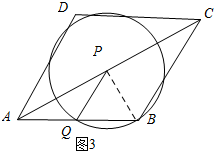
∵PQ=PB,∠PQB=60°,
∴PQ=PB=QB.
∵AQ=PQ,
∴AQ=QB=t.
∵AQ+QB=AB,
∴2t=2.
解得;t=1.
如图4所示,当圆P经过点C时.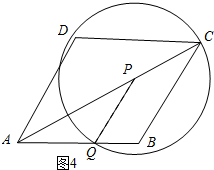
∵AQ=PQ,PQ=PC,
∴AQ=PC=t.
∵AP=$\sqrt{3}$t,
∴$\sqrt{3}$t+t=2$\sqrt{3}$.
解得:t=3-$\sqrt{3}$.
∴当1<t<3-$\sqrt{3}$时,圆P与BC只有一个交点.
综上所述,当t=4$\sqrt{3}$-6或1<t<3-$\sqrt{3}$时,圆P与BC只有一个交点.
点评 本题主要考查的是圆的综合应用,解答本题主要应用了菱形的性质、相似三角形的性质和判定、特殊锐角三角函数值、等边三角形的性质和判定,根据题意画出图形,求得圆P经过点B和点C时的t的取值是解题的关键.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
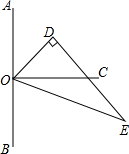 如图,点O在直线AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.
如图,点O在直线AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
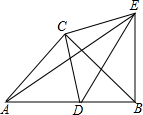 如图,△ABC和△DCE都是等腰直角三角形,∠ACB=∠DCE=∠90°,D为AB边上一点.
如图,△ABC和△DCE都是等腰直角三角形,∠ACB=∠DCE=∠90°,D为AB边上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com