
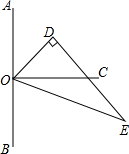
 如图,点O在直线AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.
如图,点O在直线AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.分析 (1)求出∠COE的度数,即可求出答案;
(2)根据∠AOD+COD=90°和∠COD+∠COE=90°求出∠AOD-∠COE=30°,即可得出答案;
(3)根据∠AOE=7∠COD、∠COD+∠COE=60°、∠AOE=90°+∠COE求出∠AOE=90°+60°-∠COD=150°-∠COD,即可得出关于∠AOE的方程,求出即可.
解答 解:(1)∵OC⊥AB,
∴∠AOC=90°,
∵OD在OA和OC之间,∠COD=20°,∠EOD=60°,
∴∠COE=60°-20°=40°,
∴∠AOE=90°+40°=130°,
故答案为:130°;
(2)在△ODE旋转过程中,∠AOD与∠COE大小的差不发生变化,
∵∠AOD+COD=90°,∠COD+∠COE=90°,
∴∠AOD-∠COE=90°-60°=30°,
即△ODE在想旋转过程中,∠AOD与∠COE的差不发生变化,为30°;
(3)∵∠AOE=7∠COD,∠COD+∠COE=60°,由(2)知:∠AOE=90°+∠COE,
∴∠AOE=90°+60°-∠COD=150°-∠COD,
∴∠AOE=7×150°-7∠AOE,
∴∠AOE=131.35°.
点评 本题考查了角的有关计算的应用,能根据题意求出各个角的度数是解此题的关键,题目比较好,难度不大.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:解答题
 如图,直线y=-x+2与x轴相交于点A,与y轴相交于点B.直线y=-2x+b经过点A,与y轴相交丁点C,在直线AC上是否存在点D,使∠BDA=45°?若存在,求点D的坐标;若不存在.说明理由.
如图,直线y=-x+2与x轴相交于点A,与y轴相交于点B.直线y=-2x+b经过点A,与y轴相交丁点C,在直线AC上是否存在点D,使∠BDA=45°?若存在,求点D的坐标;若不存在.说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x1=1,x2=-2 | B. | x1=0,x2=1 | C. | x1=0,x2=-1 | D. | x1=1,x2=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
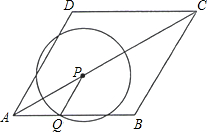 如图,菱形ABCD的边长为2cm,∠DAB=60°.点P从A点出发,以$\sqrt{3}$cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动.设点P运动的时间为ts.
如图,菱形ABCD的边长为2cm,∠DAB=60°.点P从A点出发,以$\sqrt{3}$cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动.设点P运动的时间为ts.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
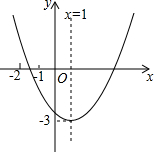 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给下以下结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给下以下结论:| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com