
分析 根据x的值计算出x2的值,将x5分解成x2•x2•x计算其值,根据题意可得a、b的值,进而可得答案.
解答 解:∵x=$\frac{\sqrt{5}-1}{2}$,
∴x2=$\frac{(\sqrt{5}-1)^{2}}{4}=\frac{6-2\sqrt{5}}{4}=\frac{3-\sqrt{5}}{2}$,
∴x5=x2•x2•x=($\frac{3-\sqrt{5}}{2}$)2•$\frac{\sqrt{5}-1}{2}$=-$\frac{19}{4}$+$\frac{7}{4}\sqrt{5}$,
又∵x5=a+b$\sqrt{5}$,且a,b均为有理数,
∴a=-$\frac{19}{4}$,b=$\frac{7}{4}$,
则a+b=-$\frac{19}{4}$+$\frac{7}{4}$=-3,
故答案为:-3.
点评 本题主要考查因式分解的应用能力,这里利用因式分解达到降幂目的是解题关键,对有理数性质得掌握是解题的根本.


 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
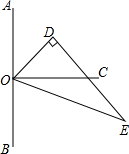 如图,点O在直线AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.
如图,点O在直线AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com