
 如图,直线y=-x+2与x轴相交于点A,与y轴相交于点B.直线y=-2x+b经过点A,与y轴相交丁点C,在直线AC上是否存在点D,使∠BDA=45°?若存在,求点D的坐标;若不存在.说明理由.
如图,直线y=-x+2与x轴相交于点A,与y轴相交于点B.直线y=-2x+b经过点A,与y轴相交丁点C,在直线AC上是否存在点D,使∠BDA=45°?若存在,求点D的坐标;若不存在.说明理由. 分析 先根据直线AC的性质断定若存在点D,点D必在线段AC上,过O作OE∥BD交AC于点E,过点O作OF⊥AE与点F,在Rt三角形AOF和OEF中用三角函数表示出OF,设出点E的坐标,根据比例关系即可得出点E的坐标,再由BC=OC-OB=2,OC=4,以及BD∥OE得出点D为线段CE的中点,再由中点坐标公式即可得出D点坐标.
解答 解:假设存在,过点O作OE∥BD交AC于点E,过点O作OF⊥AE与点F,如图.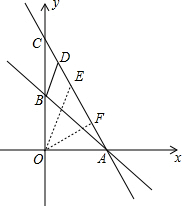
∵直线y=-x+2与x轴相交于点A,与y轴相交于点B,
∴点A(2,0),点B(0,2).
∵直线y=-2x+b经过点A,与y轴相交丁点C,
∴有0=-2×2+b,解得b=4,
∴直线AC解析式为y=-2x+4,点C(0,4).
∵tan∠OAC=$\frac{OC}{OA}$=2,
∴∠OAC>45°,∠OCA=90°-∠OAC<45°,
∴点D在线段AC上.
设E点坐标为(m,4-2m)(0<m<2).
在△OAE中,OF=OE•sin∠OEA,OF=OA•sin∠OAE,
又∵OE∥BD,tan∠OAC=2,
∴∠OEA=45°,sin∠OEA=$\frac{\sqrt{2}}{2}$,sin∠OAE=$\frac{2\sqrt{5}}{5}$,
∴OE=$\frac{2×\frac{2\sqrt{5}}{5}}{\frac{\sqrt{2}}{2}}$=$\frac{4\sqrt{10}}{5}$,
∴OE2=m2+(4-2m)2=${(\frac{4\sqrt{10}}{5})}^{2}$,
解得:m=$\frac{4}{5}$,或m=$\frac{12}{5}$(舍去),
E点坐标为($\frac{4}{5}$,$\frac{12}{5}$).
又∵BD∥OE,OB=2,OC=4,
∴B为OC中点,D为CE中点,
∵点C(0,4),点E($\frac{4}{5}$,$\frac{12}{5}$),
∴D点坐标为($\frac{2}{5}$,$\frac{16}{5}$).
故在直线AC上存在点D,使∠BDA=45°,点D的坐标为($\frac{2}{5}$,$\frac{16}{5}$).
点评 本题考查了一次函数中的动点问题,解题的关键是在△OAE中用角正弦值表示出来高线,即利用证明正弦定理的过程找到比例关系.本题属于中等难度题,失分点是不知如何将角的正弦关系转化为边的关系,在此类问题中要叫学生们明白到,只要作出高线,可以利用正弦函数表示出高,来得到边与角的正弦值之间的关系.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
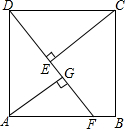 如图,正方形ABCD中,F为AB边上一点,过点A,C分别作DF的垂线,垂足为G和E,若AG=3,EG=1,则BF的长为$\frac{5}{4}$.
如图,正方形ABCD中,F为AB边上一点,过点A,C分别作DF的垂线,垂足为G和E,若AG=3,EG=1,则BF的长为$\frac{5}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
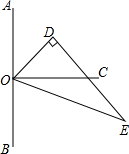 如图,点O在直线AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.
如图,点O在直线AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com