
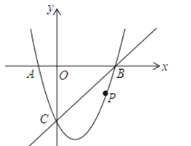
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,﹣3),点P是直线BC下方抛物线上的任意一点,过点P作平行于y轴的直线PM,交线段BC于M,当△PCM是以PM为腰的等腰三角形时,点P的坐标是( )
A.(2,-3)或(![]() +1,—2)B.(2,-3)或(
+1,—2)B.(2,-3)或(![]() ,-1-2
,-1-2![]() )
)
C.(2,-3)或(![]() ,-1-2
,-1-2![]() )D.(2,-3)或(3-
)D.(2,-3)或(3-![]() ,2-4
,2-4![]() )
)
【答案】D
【解析】
根据待定系数法,求得函数解析式,然后求出直线BC的解析式,设设M(n,n-3),P(n,n2-2n-3),分情况讨论,结合勾股定理得方程,从而解方程求得n的值,确定点P的坐标.
解:将B(3,0),C(0,-3)代入函数解析式,得
![]() ,
,
解得![]() ,
,
∴这个二次函数的表达式![]() ;
;
由题意可知:点P在第四象限
设BC的解析式为y=kx+b,
将B(3,0),C(0,-3)的坐标代入函数解析式,得![]() ,
,
解得![]() ,
,
∴BC的解析式为y=x-3,
过点P做PH⊥x轴于点H,与线段BC交于点M,连接PC
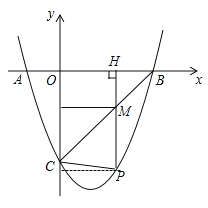
设M(n,n-3),P(n,n2-2n-3),
PM=(n-3)-(n2-2n-3)=-n2+3n=
当PM=PC时,根据勾股定理可得:
![]() ,
,
解得n1=n2=0(不符合题意,舍),n3=2,
n2-2n-3=-3,
∴P(2,-3).
当PM=MC时,根据勾股定理可得:
![]()
解得n1=0(不符合题意,舍),n2=3-![]() ,n3=3+
,n3=3+![]() (不符合题意,舍),
(不符合题意,舍),
n2-2n-3=2-4![]() ,
,
P(3-![]() ,2-4
,2-4![]() )
)
综上所述:P(2,-3)或(3-![]() ,2-4
,2-4![]() ).
).
故选:D


科目:初中数学 来源: 题型:
【题目】已知,△ABC中,AB=AC,点E是边AC上一点,过点E作EF∥BC交AB于点F
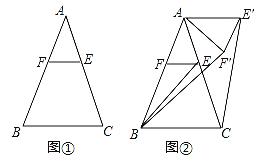
(1)如图①,求证:AE=AF;
(2)如图②,将△AEF绕点A逆时针旋转α(0°<α<144°)得到△AE′F′.连接CE′BF′.
①若BF′=6,求CE′的长;
②若∠EBC=∠BAC=36°,在图②的旋转过程中,当CE′∥AB时,直接写出旋转角α的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
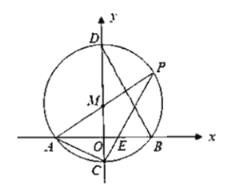
【题目】如图,在平面直角坐标系中,以点![]() 为圆心,作
为圆心,作![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于
轴于![]() 、
、![]() 两点,连结
两点,连结![]() 并延长交
并延长交![]() 于点
于点![]() ,连结
,连结![]() 交
交![]() 轴于点
轴于点![]() ,连结
,连结![]() ,
,![]() .
.
(1)求弦![]() 的长;
的长;
(2)求直线![]() 的函数解析式;
的函数解析式;
(3)连结![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
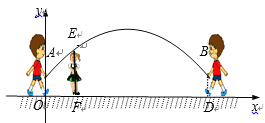
【题目】跳绳时,绳甩到最高处时的形状是抛物线. 正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0. 9米,身高为1. 4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E. 以点O为原点建立如图所示的平面直角坐标系, 设此抛物线的解析式为![]() .
.
(1)求该抛物线的解析式;
(2)如果身高为1. 85米的小华也想参加跳绳,问绳子能否顺利从他头顶越过?请说明理由;
(3)如果一群身高在1. 4米到1. 7米之间的人站在OD之间,且离点O的距离为t米, 绳子甩到最高处时必须超过他们的头顶,请结合图像,写出t的取值范围_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点M在BA的延长线上,MD切⊙O于点D,过点B作BN⊥MD于点C,连接AD并延长,交BN于点N.
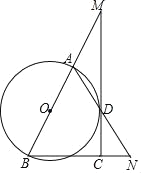
(1)求证:AB=BN;
(2)若MD=4,CD=2.4,求![]() 。
。
(3)若AM=2,CN=1.2,求⊙O的半径长。
查看答案和解析>>
科目:初中数学 来源: 题型:
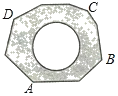
【题目】如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为2米的圆后,在附近闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下:
掷小石子落在不规则图形内的总次数 | 50 | 150 | 300 | … |
小石子落在圆内(含圆上)的次数m | 20 | 59 | 123 | … |
小石子落在圆外的阴影部分(含外缘)的次数n | 29 | 91 | 176 | … |
(1)当投掷的次数很大时,则m:n的值越来越接近 (结果精确到0.1)
(2)若以小石子所落的有效区域为总数(即m+n),则随着投掷次数的增大,小石子落在圆内(含圆上)的频率值稳定在 附近(结果精确到0.1);
(3)请你利用(2)中所得频率的值,估计整个封闭图形ABCD的面积是多少平方米?(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
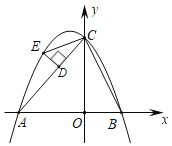
【题目】如图,已知抛物线与坐标轴交于A(﹣4,0)、B(2,0)、C(0,4),连接BC,AC.
(1)求抛物线的解析式;
(2)若点E是抛物线在第二象限上的一点,过点E作DE⊥AC于点D,求DE的最大值.
(3)若点E是抛物线上第二象限上的一动点,过点E作DE⊥AC于点D,连接CE,若△CDE与△COB相似,直接写出点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表显示的是某种大豆在相同条件下的发芽试验结果:
每批粒数n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
发芽的粒数m | 96 | 282 | 382 | 570 | 948 | 1904 | 2850 |
发芽的频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.952 | 0.950 |
下面有三个推断:
①当n为400时,发芽的大豆粒数为382,发芽的频率为0.955,所以大豆发芽的概率是0.955;
②随着试验时大豆的粒数的增加,大豆发芽的频率总在0.95附近摆动,显示出一定的稳定性,可以估计大豆发芽的概率是0.95;
③若大豆粒数n为4000,估计大豆发芽的粒数大约为3800粒.
其中推断合理的是( )
A. ①②③ B. ①② C. ①③ D. ②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com