
【题目】如图,已知抛物线 ![]() 与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,有一宽度为1的刻度尺沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q,交直线AC于点M和点N,交x轴于点E和点F.
与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,有一宽度为1的刻度尺沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q,交直线AC于点M和点N,交x轴于点E和点F.
(1)求点A、B、C的坐标;
(2)当点M和点N都在线段AC上时,连接EN,如果点E的坐标为(4,0),求sin∠ANE的值;
(3)在刻度尺平移过程中,当以点P、Q、N、M为顶点的四边形是平行四边形时,求点N的坐标.
【答案】
(1)
解:令y=0得: ![]() =0,解得x=5或x=﹣3.
=0,解得x=5或x=﹣3.
∵点A在点B的右侧,
∴点A、B的坐标分为(5,0)、(﹣3,0).
当x=0时,y=5,
∴点C的坐标为(0,5)
(2)
解:如图1,作EG⊥AC,垂足为点G.
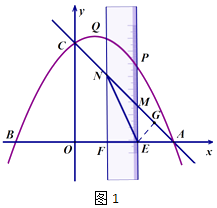
∵点E的坐标为(4,0),
∴OE=4.
∵OA=OC=5,
∴AE=1,∠OAC=45°.
∴AF=FN=2,GE=AEsin45°= ![]()
在Rt△EFN中,依据勾股定理可知NE= ![]() =
= ![]() ,
,
∴sin∠ANE= ![]() =
= ![]() =
= ![]()
(3)
解:设直线AC的函数表达式为y=kx+b.
将点A和点C的坐标代入得: ![]() ,
,
解得k=﹣1,b=5.
∴直线AC的函数表达式为y=﹣x+5.
①当MN为边时,如图2所示:
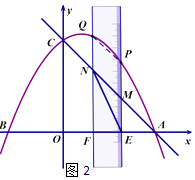
设点Q(n, ![]() ),
),
则点P(n+1, ![]() ),点N(n,﹣n+5)M(n+1,﹣n+4).
),点N(n,﹣n+5)M(n+1,﹣n+4).
∵QN=PM
∴ ![]() ,解得n=2.
,解得n=2.
∴点N的坐标为(2,3).
②当MN是平行四边形的对角线时,如图3所示:
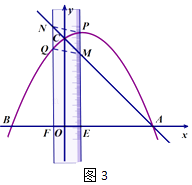
设点F的坐标为(m,0),
则N(m,﹣m+5),M(m+1,﹣m+4),
Q(m, ![]() ),P(m+1,
),P(m+1, ![]() ).
).
∵QN=PM,
∴ ![]() ,解得m=2±
,解得m=2± ![]() .
.
∴点N的坐标为(2+ ![]() ,3﹣
,3﹣ ![]() )或(2﹣
)或(2﹣ ![]() ,3+
,3+ ![]() ).
).
综上所述,以点P、Q、N、M为顶点的四边形是平行四边形时,点N的坐标为(2,3)
或(2+ ![]() ,3﹣
,3﹣ ![]() )或(2﹣
)或(2﹣ ![]() ,3+
,3+ ![]() )
)
【解析】(1)利用坐标轴上点的坐标特征即可结论;(2)先确定出AF=FN=2,GE= ![]() ,再利用勾股定理求出NE=
,再利用勾股定理求出NE= ![]() ,即可得出结论;(3)先确定出直线AC的函数表达式为y=﹣x+5.再分MN为边和对角线两种情况,建立方程求解即可得出结论.
,即可得出结论;(3)先确定出直线AC的函数表达式为y=﹣x+5.再分MN为边和对角线两种情况,建立方程求解即可得出结论.
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案,需要熟知二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】已知函数y=mx2﹣(2m﹣5)x+m﹣2的图象与x轴有两个公共点.
(1)求m的取值范围,并写出当m取范围内最大整数时函数的解析式;
(2)题(1)中求得的函数记为C1 ,
①当n≤x≤﹣1时,y的取值范围是1≤y≤﹣3n,求n的值;
②函数C2:y=m(x﹣h)2+k的图象由函数C1的图象平移得到,其顶点P落在以原点为圆心,半径为 ![]() 的圆内或圆上,设函数C1的图象顶点为M,求点P与点M距离最大时函数C2的解析式.
的圆内或圆上,设函数C1的图象顶点为M,求点P与点M距离最大时函数C2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社拟在暑假期间面向学生推出“林州红旗渠一日游”活动,
收费标准如下:
人数m | 0<m≤100 | 100<m≤200 | m>200 |
收费标准(元/人) | 90 | 85 | 75 |
甲、乙两所学校计划组织本校学生自愿参加此项活动.已知甲校报名参加的学生人数多于100人,乙校报名参加的学生人数少于100人.经核算,若两校分别组团共需花费10 800元,若两校联合组团只需花赞18 000元.
(1)两所学校报名参加旅游的学生人数之和超过200人吗? 为什么?
(2)两所学校报名参加旅游的学生各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店张阿姨以每斤4元的价格购进某种水果若干斤,然后以每斤6元的价格出售,每天可售出150斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出30斤,为保证每天至少售出360斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利450元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,填空:
(1)若∠4=∠3,则____∥_____,理由是______;
(2)若∠2=∠E,则____∥___,理由是____;
(3)若∠A=∠ABE=180°,则____∥___,理由是____;
(4)若∠2=∠____,则DA∥EB,理由是____;
(5)若∠DBC+∠_____=180°,则DB∥EC,理由是____;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级某班同学在毕业晚会中进行抽奖活动,在一个不透明的口袋中有三个完全相同的小球,把它们分别标号为1,2,3.随机摸出一个小球记下标号后放回摇匀,再从中随机摸出一个小球记下标号.
(1)请用列表或画树形图的方法(只选其中一样),表示两次摸出小球上的标号的所有结果;
(2)规定当两次摸出的小球标号相同时中奖,求中奖的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为表彰在某活动中表现积极的同学,老师决定购买文具盒与钢笔作为奖品.已知5个文具盒、2支钢笔共需100元;3个文具盒、1支钢笔共需57元.
(1)每个文具盒、每支钢笔各多少元?
(2)若本次表彰活动,老师决定购买10件作为奖品,若购买![]() 个文具盒,10件奖品共需
个文具盒,10件奖品共需![]() 元,求
元,求![]() 与
与![]() 的函数关系式.如果至少需要购买3个文具盒,本次活动老师最多需要花多少钱?
的函数关系式.如果至少需要购买3个文具盒,本次活动老师最多需要花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
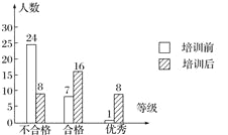
【题目】某校学生在电脑培训前后各参加了一次水平相同的考试,考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级.为了了解电脑培训的效果,随机抽取其中32名学生两次考试考分等级制成统计图(如图),试回答下列问题:
(1)这32名学生经过培训,考分等级“不合格”的百分比由________下降到________;
(2)估计该校640名学生,培训后考分等级为“合格”与“优秀”的学生共有多少名.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com