
【题目】如图,大海中有两个岛屿A与B,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°,在点F处测得∠AFP=60°,∠BFQ=60°.
(1)判断AE,AB的数量关系,并说明理由;
(2)求∠BAE的度数.

【答案】(1)见解析;(2) 28°.
【解析】
(1)在△EOF中,根据三角形内角和定理得出∠EOF=90°.在△EBF中,根据外角的性质得出∠EBF=30°,根据等角对等边得到EF=BF,由等腰三角形三线合一的性质得到AF垂直平分BE,由线段垂直平分线的性质即可得到结论;
(2)由三角形外角的性质得出∠EAO的度数,再由等腰三角形三线合一的性质即可得到结论.
(1)AE=AB.理由如下:
∵∠BEF=30°,∠AFE=60°,∴∠EOF=90°.
∵∠BFQ=60°,∠BEF=30°,∴∠EBF=30°,∴BF=EF,∴OE=OB,即AF垂直平分BE,∴AE=AB;
(2)∵∠AEP=74°,∠AFP=60°,∴∠EAF=74°-60°=14°.
∵AE=AB,AF⊥BE,∴∠EAO=∠BAO,∴∠BAE=2∠EAO =2∠EAF=28°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是 (请将所有正确结论的序号都填上).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,以AB为直径的⊙O分别交边BC、AC于点D、点E,且AE=BE.
(1)如图①,求∠EBC的度数; 
(2)如图②,过点D作⊙O的切线交AB的延长线于点G,交AC于点F,若⊙O的直径为10,求BG的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公园门票价格规定如下:

某校七年级(1)(2)两个班共104人去游园,其中(1)班有40多人,且不足50人,经估算,如果两个班都以班为单位进行购票,则一共应付1240元,问:
(1)两个班各有多少个学生?
(2)如果两班联合起来,作为一个团体票能省多少钱?如果七(1)班单独组织去游园,作为组织者的你如何购票才最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,
,![]() 平分
平分![]() ,给出下列结论:
,给出下列结论:
①当![]() 时,
时,![]() ;
;
②![]() 为
为![]() 的平分线;
的平分线;
③与![]() 相等的角有三个;
相等的角有三个;
④![]() .
.
其中正确的结论为

A. ①②④ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列每个图形及相应推出的结论,其中正确的是( )
A.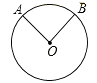
∵ ![]()
∴∠AOB=80°
B.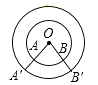
∵∠AOB=∠A′O′B′
∴ ![]()
C.
∵ ![]()
∴AB=CD
D.
∵MN垂直平分AD
∴ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的个数有( )
BC,成立的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1,可以得到![]() 这个等式,请解答下列问题:
这个等式,请解答下列问题:

(1)写出图2中所表示的数学等式______________;(最后结果)
(2)根据整式乘法的运算法则,通过计算验证上述等式;
(3)利用(1)中得到的结论,解决问题:若a+b+c=10,ab+ac+bc=35,求a2+b2+c2的值;
(4)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形,z张边长分别为a、b的长方形纸片拼出一个面积为(5a+2b)(3a+5b)的长方形,求x+y+z的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com