
����Ŀ����1�����߶�AC=30mm����A����ࣩ��
��2����CΪ���㣬CAΪһ�ߣ�����ACM=90�㣻
��3����AΪ���㣬ACΪһ�ߣ��ڡ�ACM��ͬ���CAN=60�㣬AN��CM�ཻ�ڵ�B������AB�Ƕ���mm��
��4������AB�е�D������DC����ʱ����DC�Ƕ���mm���������AB��DC��������ϵ�ǣ�AB��DC�Ķ��ٱ���
��5������D��ֱ��BC�ľ���DE��������DE���ڶ���mm���������DE��AC��������ϵ�ǣ�DE��AC��������ϵ�ǣ���λ�ù�ϵ�ǣ���
���𰸡��⣺��1����������������AO��
��������AO�Ͻ�ȡ�߶�AC=30mm��
��2����������CΪ���㣬������������á�ACM=90�㣻
��3����������AΪ���㣬������������á�CAN=60�㣻
��ֱ��������ABC�У���CAB=60�㣬AC=30mm��
��AB=AC��cos��CAB=60mm��
��4������������ֱ�ߣ���A��Ϊ��㣬����AD=30mm����D��Ϊ����
��ֱ��������ABC�У�CDΪб��AB�ϵ����ߣ�
��CD=![]() AB=30mm��
AB=30mm��
��AB=2DC��
��5������������D��DE��AC��CM�ڵ�E��DE��Ϊ����
��DE��BC��AC��BC��
��DE��AC��
��DE��AC=BD��AC=1��2��
��DE=![]() AC=15mm��
AC=15mm��
�ʴ�Ϊ����3��60����4��30��2����5��15��![]() ��ƽ�У�
��ƽ�У�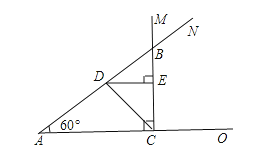
����������1������ֱ����ͼ��
��2��������������ͼ��
��3��������������á�CAN=60�㣬Ȼ��������Ǻ������AB�ij��ȣ�
��4������ֱ�߲��AB���е�D��Ȼ����ֱ��������ABC����б��AB�ϵ�����CD�ij��ȼ�б��AB��б��������CD�Ĺ�ϵ��
��5������D��AC��ƽ����DE��Ȼ�����ƽ���ߵ����ʣ���ֱ��ƽ�У���Ӧ�߶γɱ���������DE�ij��ȣ�
�����㾫����������Ĺؼ���������ƽ���ߵ��ж������֪ʶ������ͬλ����ȣ���ֱ��ƽ��;�ڴ�����ȣ���ֱ��ƽ��;ͬ���ڽǻ�������ֱ��ƽ�У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�E��F�ֱ���AB��AC���е㣬��EF=3��������ABCD���ܳ��ǣ� �� 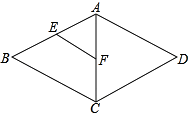
A.12
B.16
C.20
D.24
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ�ij�31��4cm����5cm�ij����Σ�Χ��һ��Բ���壬������ϵ���������Բ������Ƕ���ƽ�����ף� ![]()
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������˵���У���ȷ���ǣ�������
A.��Ϊ��A+��D=180�㣬����AD��BC
B.��Ϊ��C+��D=180�㣬����AB��CD
C.��Ϊ��A+��D=180�㣬����AB��CD
D.��Ϊ��A+��C=180�㣬����AB��CD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����н���100m��ʾ��������(����)��
A. ���н�100m B. �����н�100m C. ���н�100m D. �����н�100m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ô���ʽ��ʾa��b�����ĺ���a��b�����IJ�Ļ��ǣ� ��
A.��a+b����a��b��
B.��a+b��a��b
C.a��a+b����b
D.��a+b����ab
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�ס�A'B'C'��AD��A'D'�����ǵĶ�Ӧ���ߣ���AD��10��A'D'��6�����ABC���A'B'C'���ܳ����ǣ�������
A. 3��5B. 9��25C. 5��3D. 25��9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Խ��Խ��س�Ϊ���ǵ�һ�����ѷ�ʽ����2018�����˫11�����ϴ��������è���Ա���֧������ͻ��220000000000Ԫ��������220000000000�ÿ�ѧ��������ʾΪ_________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���B=90�㣬��E��AC���е㣬AC=2AB����BAC��ƽ����AD��BC�ڵ�D����AF��BC������DE���ӳ���AF�ڵ�F������FC��
��֤���ı���ADCF�����Σ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com