
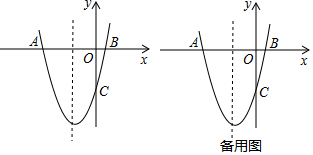
���� ��1�������⣬�ɵ�A��-5��0����C��0��-5�����ѵ�A��C���������y=x2+bx+c���õ�����b��c�Ķ�Ԫһ�η����飬�ⷽ���鼴����������ߵĺ�������ʽ��
��2�������䷽����������ߵĶԳ�����ֱ��x=-2����������y=x2+4x-5��x�ύ�ڵ�A��B���ó���A��B����ֱ��x=-2�Գƣ�����AC�����Գ����ڵ�P����������֮���߶���̿�֪��ʱPB+PC��ֵ��С�����ô���ϵ�������ֱ��AC�Ľ���ʽΪy=-x-5����x=-2���룬���y=-3�������ó���P�����ꣻ
��3���ڣ�2�������£���P������Ϊ��-2��-3������F��x��x2+4x-5�������������ε����ʿɵ�E��-2��x2+4x-5����M��x��-3����PM=PE�����������ľ��빫ʽ�г�����|x+2|=|x2+4x-5+3|���ⷽ�̼�����⣮
��� �⣺��1�������⣬�ɵ�A��-5��0����C��0��-5����
��������y=x2+bx+c����A����C��
��$\left\{\begin{array}{l}{25-5b+c=0}\\{c=-5}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=4}\\{c=-5}\end{array}\right.$��
�������߶�Ӧ�ĺ�������ʽΪy=x2+4x-5��
��2����y=x2+4x-5=��x+2��2-9��
��Գ�����ֱ��x=-2��
��������y=x2+4x-5��x�ύ�ڵ�A��B��
���A��B����ֱ��x=-2�Գƣ�
����AC�����Գ����ڵ�P����ʱPB+PC��ֵ��С��
��ֱ��AC�Ľ���ʽΪy=mx+n��
��$\left\{\begin{array}{l}{-5m+n=0}\\{n=-5}\end{array}\right.$�����$\left\{\begin{array}{l}{m=-1}\\{n=-5}\end{array}\right.$��
��ֱ��AC�Ľ���ʽΪy=-x-5��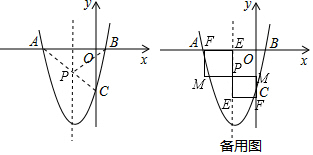 ��x=-2ʱ��y=-3��
��x=-2ʱ��y=-3��
���P��������-2��-3����
��3���ڣ�2�������£���P������Ϊ��-2��-3����
��F��x��x2+4x-5����
���ı���PEFMΪ�����Σ�
��E��-2��x2+4x-5����M��x��-3����PM=PE��
��|x+2|=|x2+4x-5+3|��
��x2+4x-2=x+2����x2+4x-2=-x-2��
������x2+3x-4=0����x2+5x=0��
���x1=-4��x2=1��x3=0��x4=-5��
��M��-4��-3����M��1��-3����M��0��-3����M��-5��-3����
���� �����Ƕ��κ����ۺ��⣬�����漰�����ô���ϵ��������������ֱ�ߵĽ���ʽ�����κ��������ʣ���ԳƵ����ʣ������ε����ʣ��ۺ��Խ�ǿ���Ѷ����У��������ν���뷽��˼���ǽ���Ĺؼ���


 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д� ����ѵ��ϵ�д�
����ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��һ�����������أ���үү����������طֳ������ȵ��Ŀ�������ĸ����Ӹ��֣���������ƶ������ֻ��ַ�������ѡ��ͼ˵������
��һ�����������أ���үү����������طֳ������ȵ��Ŀ�������ĸ����Ӹ��֣���������ƶ������ֻ��ַ�������ѡ��ͼ˵�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����3�Ų����Ŀ�Ƭ��������д�в�ͬ�������⣬��������ͬ������3�ſ�Ƭ��������ϴ�ȣ����������ȡһ�ţ��������ֺ�Żأ�����ϴ�Ⱥ��ٴ��������ȡһ�ţ�����ȡ�ĵ�һ�š��ڶ��ſ�Ƭ�ϵ����ֱַ���Ϊʮλ���ֺ�λ���������λ����
��ͼ����3�Ų����Ŀ�Ƭ��������д�в�ͬ�������⣬��������ͬ������3�ſ�Ƭ��������ϴ�ȣ����������ȡһ�ţ��������ֺ�Żأ�����ϴ�Ⱥ��ٴ��������ȡһ�ţ�����ȡ�ĵ�һ�š��ڶ��ſ�Ƭ�ϵ����ֱַ���Ϊʮλ���ֺ�λ���������λ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AB�ǡ�O��ֱ����CD���O�����ڵ�C����AB���ӳ��߽���D��
��ͼ��AB�ǡ�O��ֱ����CD���O�����ڵ�C����AB���ӳ��߽���D���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com