
【题目】如图,A、B、C分别是线段A1B、B1C、C1A的中点,若△A1BlC1的面积是14,那么△ABC的面积是( )

A.2B.![]() C.3D.
C.3D.![]()
【答案】A
【解析】
连接AB1,BC1,CA1,根据等底等高的三角形的面积相等求出△ABB1,△A1AB1的面积,从而求出△A1BB1的面积,同理可求△B1CC1的面积,△A1AC1的面积,于是得到结论.
如图,连接AB1,BC1,CA1,

∵A、B分别是线段A1B,B1C的中点,
∴S△ABB1=S△ABC,
S△A1AB1=S△ABB1=S△ABC,
∴S△A1BB1=S△A1AB1+S△ABB1=2S△ABC,
同理:S△B1CC1=2S△ABC,S△A1AC1=2S△ABC,
∴△A1B1C1的面积=S△A1BB1+S△B1CC1+S△A1AC1+S△ABC=7S△ABC=14.
∴S△ABC=2,
故选A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=![]() BC,连接CD和EF.
BC,连接CD和EF.

(1)求证:DE=CF;
(2)求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市举行店庆活动,对甲、乙两种商品实行打折销售,打折前,购买2件甲商品和3件乙商品需要180元;购买1件甲商品和4件乙商品需要200元,而店庆期间,购买10件甲商品和10件乙商品仅需520元,这比打折前少花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移6个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度) .

(1)在图中画出平移后的△A1B1C1;
(2)直接写出△A1B1C1各顶点的坐标.
![]() ;
; ![]() ;
; ![]() ;
;
(3)求出△ABC的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市对位于笔直公路AC上两个小区A,B的供水路线进行优化改造,供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A,B之间的距离为300(![]() +1)米,求供水站M分别到小区A,B的距离.(结果可保留根号)
+1)米,求供水站M分别到小区A,B的距离.(结果可保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:![]() 分别与x轴、y轴交于点B、C,且与直线l2:
分别与x轴、y轴交于点B、C,且与直线l2:![]() 交于点A.
交于点A.
(1)求出点A的坐标
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC,PF⊥CD,垂足分别为点E,F,连接AP,EF,给出下列四个结论:

①AP=EF;②∠PFE=∠BAP;③PD=![]() EC;④△APD一定是等腰三角形.
EC;④△APD一定是等腰三角形.
其中正确的结论有( ).
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
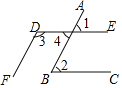
【题目】如图,∠1=60°,∠2=60°,∠3=120°.
试说明DE∥BC,DF∥AB,根据图形,完成下列推理:
∵∠1=60°,∠2=60°(已知)
∴∠1=∠2(等量代换)
∴ ∥ ( )
∵AB,DE相交,
∴∠4=∠1=60°
∵∠3=120°
∴∠3+∠4=180°
∴ ∥ ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,点
两点,点![]() 是
是![]() 轴上一动点,要使点
轴上一动点,要使点![]() 关于直线
关于直线![]() 的对称点刚好落在
的对称点刚好落在![]() 轴上,则此时点
轴上,则此时点![]() 的坐标是( )
的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com