
【题目】如图,在平面直角坐标系中,反比例函数![]() (x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为6,则k= .
(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为6,则k= .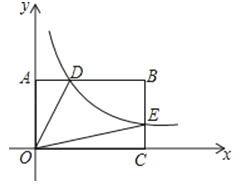
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】理解:数学兴趣小组在探究如何求tan15°的值,经过思考、讨论、交流,得到以下思路:
思路一 如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB至点D,使BD=BA,连接AD.设AC=1,则BD=BA=2,BC=![]() .tanD=tan15°=
.tanD=tan15°=![]() =
=![]() =2﹣
=2﹣![]() .
.
思路二 利用科普书上的和(差)角正切公式:tan(α±β)=![]() .假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=
.假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=![]() =
=![]() =2﹣
=2﹣![]() .
.
思路三 在顶角为30°的等腰三角形中,作腰上的高也可以…
思路四 …
请解决下列问题(上述思路仅供参考).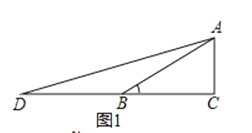
(1)类比:求出tan75°的值;
(2)应用:如图2,某电视塔建在一座小山上,山高BC为30米,在地平面上有一点A,测得A,C两点间距离为60米,从A测得电视塔的视角(∠CAD)为45°,求这座电视塔CD的高度;
(3)拓展:如图3,直线y=![]() x﹣1与双曲线y=
x﹣1与双曲线y=![]() 交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.
交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.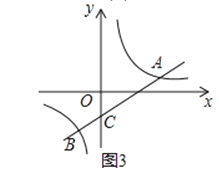
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(﹣1,0),点C的坐标是(0,﹣3)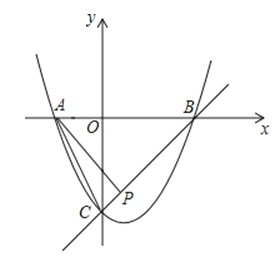
(1)求抛物线的函数表达式.
(2)求直线BC的函数表达式和∠ABC的度数.
(3)P为线段BC上一点,连接AC,AP,若∠ACB=∠PAB,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C、D分别在扇形AOB的半径OA、OB的延长线上,且OA=3,AC=3 ![]() ﹣3,CD∥AB,并与弧AB相交于点M、N.
﹣3,CD∥AB,并与弧AB相交于点M、N. 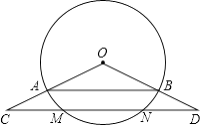
(1)求线段OD的长;
(2)若sin∠C= ![]() ,求弦MN的长;
,求弦MN的长;
(3)在(2)的条件下,求优弧MEN的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
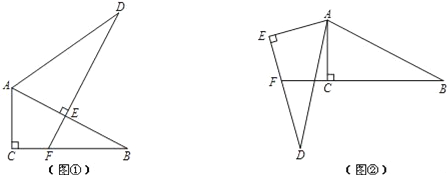
【题目】已知Rt△ABC≌Rt△ADE,其中∠ACB=∠AED=90°.
(1)将这两个三角形按图①方式摆放,使点E落在AB上,DE的延长线交BC于点F.求证:BF+EF=DE;
(2)改变△ADE的位置,使DE交BC的延长线于点F(如图②),则(1)中的结论还成立吗?若成立,加以证明;若不成立,写出此时BF、EF与DE之间的等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列解答中,填写适当的理由或数学式:

(1)∵ ∠ABD=∠CDB, ( 已知 )
∴ ∥ . ( )
(2)∵ ∠ADC+∠DCB=180°, ( 已知 )
∴ ∥ . ( )
(3)∵ AD∥BE, ( 已知 )
∴ ∠DCE=∠ . ( )
(4)∵ ∥ , ( 已知 )
∴ ∠BAE=∠CFE. ( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com