
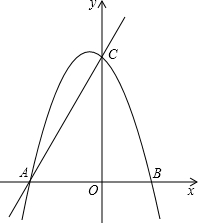
 ��ͼ��ʾ����ֱ֪��y=kx+m��x�ᡢy��ֱ���A��C���㣬������y=-x2+bx+c����A��C���㣬��B����������x�����һ�����㣬��x=-$\frac{1}{2}$ʱ��yȡ���ֵ$\frac{25}{4}$��
��ͼ��ʾ����ֱ֪��y=kx+m��x�ᡢy��ֱ���A��C���㣬������y=-x2+bx+c����A��C���㣬��B����������x�����һ�����㣬��x=-$\frac{1}{2}$ʱ��yȡ���ֵ$\frac{25}{4}$������ ��1���ȸ���������y=-x2+bx+c����x=-$\frac{1}{2}$ʱ��yȡ���ֵ$\frac{25}{4}$���õ������ߵĶ�������Ϊ��-$\frac{1}{2}$��$\frac{25}{4}$������д�������ߵĶ���ʽ���ٸ��������ߵĽ���ʽ���A��C�����꣬���ô���ϵ�����������ֱ�ߵĽ���ʽ��
��2�����ݵȸ������ε�����ȵ��ڵױ߱ȣ�����������ε������ʵ����AP��PC=1��3����3AP=PC���������AC�ij���Ȼ���������ۣ�
�ٵ�P���߶�AC��ʱ������P��PH��x�ᣬ��HΪ���㣮��PH��OC������ƽ���߷��߶γɱ����������PH�ij����������P������ꣻ
�ڵ�P��CA���ӳ�����ʱ����PG��OC������ƽ���߷��߶γɱ����������PG�ij����������P������ꣻ
��3�������������Ľ���ʽ����ֱ��y=$\frac{1}{2}$x+a��������y=-x2-x+6�Ľ���ΪM��xM��yM����N��xN��yN����M��N��ࣩ����xM��xN�Ƿ���x2+$\frac{3}{2}$x+a-6=0������������һԪ���η��̸���ϵ����ϵ�ã�xM+xN=-$\frac{3}{2}$��xM•xN=a-6���������yM•yN=$\frac{1}{4}$��a-6��-$\frac{3}{4}$a+a2��
�����ڡ�MON=90�㣬���ݹ��ɶ����ó�OM2+ON2=MN2���ݴ��г�����a�ķ��̣��ⷽ�̼������a��ֵ��
�����ڡ�MON��90�㣬���ݹ��ɶ����ó�OM2+ON2��MN2���ݴ��г�����a�IJ���ʽ���ⲻ��ʽ�������a�ķ�Χ��
��� �⣺��1����������y=-x2+bx+c��
��x=-$\frac{1}{2}$ʱ��yȡ���ֵ$\frac{25}{4}$��
�������ߵĽ���ʽ�ǣ�y=-��x+$\frac{1}{2}$��2+$\frac{25}{4}$����y=-x2-x+6��
��x=0ʱ��y=6����C�������ǣ�0��6����
��y=0ʱ��-x2-x+6=0����ã�x=2��-3��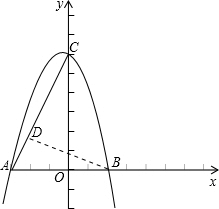 ��A�������ǣ�-3��0����B�������ǣ�2��0����
��A�������ǣ�-3��0����B�������ǣ�2��0����
��A��-3��0����C��0��6������ֱ��AC�Ľ���ʽy=kx+m��
��$\left\{\begin{array}{l}{-3k+m=0}\\{m=6}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=2}\\{m=6}\end{array}\right.$��
��ֱ�ߵĽ���ʽ�ǣ�y=2x+6��
��2������B��BD��AC��DΪ���㣬
��S��ABP��S��BPC=1��3��
��$\frac{\frac{1}{2}AP•BD}{\frac{1}{2}PC•BD}$=$\frac{1}{3}$��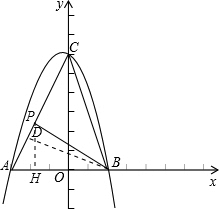 ��AP��PC=1��3��
��AP��PC=1��3��
�ɹ��ɶ�������AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=3$\sqrt{5}$��
�ٵ���PΪ�߶�AC��һ��ʱ������P��PH��x�ᣬ��HΪ���㣮
��PH��OC��
��$\frac{PH}{OC}$=$\frac{AP}{AC}$=$\frac{1}{4}$��
��PH=$\frac{3}{2}$��
��$\frac{3}{2}$=2x+6��
��x=-$\frac{9}{4}$��
���P��-$\frac{9}{4}$��$\frac{3}{2}$����
��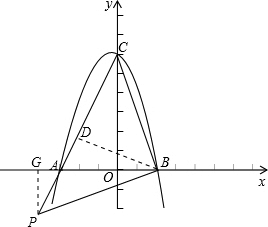 ����P��CA�ӳ���ʱ����PG��x�ᣬ��GΪ���㣮
����P��CA�ӳ���ʱ����PG��x�ᣬ��GΪ���㣮
��AP��PC=1��3��
��AP��AC=1��2��
��PG��OC��
��$\frac{PG}{OC}$=$\frac{AP}{AC}$=$\frac{1}{2}$��
��PG=3��
��-3=2x+6��x=-$\frac{9}{2}$��
���P��-$\frac{9}{2}$��-3����
������������P��������-$\frac{9}{4}$��$\frac{3}{2}$����-$\frac{9}{2}$��-3����
��3����ֱ��y=$\frac{1}{2}$x+a��������y=-x2-x+6�Ľ���ΪM��xM��yM����N��xN��yN����M��N��ࣩ��
��$\left\{\begin{array}{l}{{x}_{1}={x}_{M}}\\{{y}_{1}={y}_{M}}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}={x}_{N}}\\{{y}_{2}={y}_{N}}\end{array}\right.$Ϊ������$\left\{\begin{array}{l}{y=\frac{1}{2}x+a}\\{y=-{x}^{2}-x+6}\end{array}\right.$�Ľ⣬
�ɷ�������ȥy�������ã�x2+$\frac{3}{2}$x+a-6=0��
��xM��xN�Ƿ���x2+$\frac{3}{2}$x+a-6=0����������
��xM+xN=-$\frac{3}{2}$��xM•xN=a-6��
��yM•yN=��$\frac{1}{2}$xM+a����$\frac{1}{2}$xN+a��=$\frac{1}{4}$xM•xN+$\frac{a}{2}$��xM+xN��+a2=$\frac{1}{4}$��a-6��-$\frac{3}{4}$a+a2��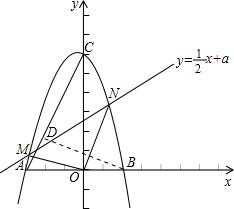 �ٴ���a��ֵ��ʹ�á�MON=90�㣮�������£�
�ٴ���a��ֵ��ʹ�á�MON=90�㣮�������£�
�ߡ�MON=90�㣬
��OM2+ON2=MN2����${x}_{M}^{2}$+${y}_{M}^{2}$+${x}_{N}^{2}$+${y}_{N}^{2}$=��xM-xN��2+��yM-yN��2��
�����xM•xN+yM•yN=0��
�ࣨa-6��+$\frac{1}{4}$��a-6��-$\frac{3}{4}$a+a2=0��
��������2a2+a-15=0��
���a1=-3��a2=$\frac{5}{2}$��
�����aֵ��ʹ�á�MON=90�㣬��ֵΪa=-3��a=$\frac{5}{2}$��
�ڡߡ�MON��90�㣬
��OM2+ON2��MN2����${x}_{M}^{2}$+${y}_{M}^{2}$+${x}_{N}^{2}$+${y}_{N}^{2}$����xM-xN��2+��yM-yN��2��
�����xM•xN+yM•yN��0��
�ࣨa-6��+$\frac{1}{4}$��a-6��-$\frac{3}{4}$a+a2��0��
��������2a2+a-15��0��
���-3��a��$\frac{5}{2}$��
�൱��MON��90��ʱ��a��ȡֵ��Χ��-3��a��$\frac{5}{2}$��
���� ���⿼���˶��κ������ۺ����ͣ������漰�����ô���ϵ���������Ľ���ʽ�����κ��������ʣ������ε������ƽ���߷��߶γɱ��������������뷽�̵Ĺ�ϵ�����ɶ������۽����������ߵĹ�ϵ��֪ʶ���ۺ��Խ�ǿ���ѶȽϴ����÷������ۡ����ν�ϼ�����˼���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ı���OABC�ı�OA��OC�ֱ���y�ᡢx��������ᣬ��OA=OC=3����OCB=90�㣬AB=$\sqrt{10}$��
��ͼ���ı���OABC�ı�OA��OC�ֱ���y�ᡢx��������ᣬ��OA=OC=3����OCB=90�㣬AB=$\sqrt{10}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
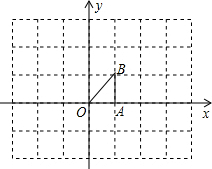 ��ͼ����ֱ������ϵ�еġ�OAB������A��1��0����B��1��1����
��ͼ����ֱ������ϵ�еġ�OAB������A��1��0����B��1��1�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 30�� | B�� | 45�� | C�� | 60�� | D�� | 75�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a6•a6=2a6 | B�� | 2m+3n=6m+n | C�� | ��a-b��5��b-a��4=��a-b�� | D�� | -a3•��-a��5=a8 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com