
分析 根据完全平方公式,可得非负数的和为零,可得每个非负数为零,可得a、b、c的值,根据勾股定理逆定理,可得答案.
解答 解:△ABC是等腰直角三角形.
理由:∵a2-4a+b2-4$\sqrt{2}$c=4b-16-c2,
∴(a2-4a+4)+(b2-4b+4)+(c2-4$\sqrt{2}$c+8)=0,
即:(a-2)2+(b-2)2+(c-2$\sqrt{2}$)2=0.
∵(a-2)2≥0,(b-2)2≥0,(c-2$\sqrt{2}$)2≥0,
∴a-2=0,b-2=0,c-2$\sqrt{2}$=0,
∴a=b=2,c=2$\sqrt{2}$,
∵22+22=(2$\sqrt{2}$)2,
∴a2+b2=c2,
所以△ABC是以c为斜边的等腰直角三角形.
点评 本题考查了因式分解的应用,勾股定理逆定理,利用了非负数的和为零得出a、b、c的值是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD中,点E是AD的中点,连接BE、CE,点F是CE的中点,连接DF、
如图,在正方形ABCD中,点E是AD的中点,连接BE、CE,点F是CE的中点,连接DF、查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,二次函数y1=a(x-2)2的图象与直线交于A(0,-1),B(2,0)两点.
如图,二次函数y1=a(x-2)2的图象与直线交于A(0,-1),B(2,0)两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
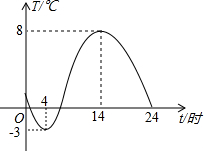 如图,是一台自动测温记录仪的图象,它反映了嵊州市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )
如图,是一台自动测温记录仪的图象,它反映了嵊州市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )| A. | 凌晨4时气温最低为-3℃ | |
| B. | 从0时至14时,气温随时间增长而上升 | |
| C. | 14时气温最高为8℃ | |
| D. | 从14时至24时,气温随时间增长而下降 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com