
ЁОЬтФПЁПШчЭМ1ЃЌНЋСНИіЕШбќШ§НЧаЮ![]() КЭ
КЭ![]() ЦДКЯдквЛЦ№ЃЌЦфжа
ЦДКЯдквЛЦ№ЃЌЦфжа![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .
.
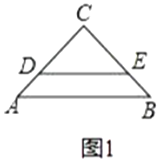
ЃЈ1ЃЉВйзїЗЂЯж
ШчЭМ2ЃЌЙЬЖЈ![]() ЃЌАб
ЃЌАб![]() ШЦзХЖЅЕу
ШЦзХЖЅЕу![]() а§зЊЃЌЪЙЕу
а§зЊЃЌЪЙЕу![]() Тфдк
Тфдк![]() БпЩЯ.
БпЩЯ.
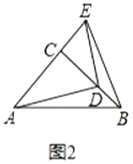
ЬюПеЃКЯпЖЮ![]() гы
гы![]() ЕФЙиЯЕЪЧЂйЮЛжУЙиЯЕЃК______ЃЛЂкЪ§СПЙиЯЕЃК______
ЕФЙиЯЕЪЧЂйЮЛжУЙиЯЕЃК______ЃЛЂкЪ§СПЙиЯЕЃК______
ЃЈ2ЃЉБфЪНЬНОП
ЕБ![]() ШЦЕу
ШЦЕу![]() а§зЊЕНЭМ3ЕФЮЛжУЪБЃЌЃЈ1ЃЉжаЕФНсТлЛЙГЩСЂТ№ЃПЧыЫЕУїРэгЩЃЛ
а§зЊЕНЭМ3ЕФЮЛжУЪБЃЌЃЈ1ЃЉжаЕФНсТлЛЙГЩСЂТ№ЃПЧыЫЕУїРэгЩЃЛ
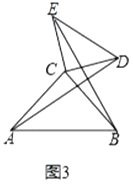
ЃЈ3ЃЉНтОіЮЪЬт
ШчЭМ4ЃЌвбжЊЯпЖЮ![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() ЃЌвд
ЃЌвд![]() ЮЊБпзївЛИіе§ЗНаЮ
ЮЊБпзївЛИіе§ЗНаЮ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЫцзХБп
ЃЌЫцзХБп![]() ЕФБфЛЏЃЌЯпЖЮ
ЕФБфЛЏЃЌЯпЖЮ![]() ЕФГЄвВЛсЗЂЩњБфЛЏ.ЧыжБНгаДГіЯпЖЮ
ЕФГЄвВЛсЗЂЩњБфЛЏ.ЧыжБНгаДГіЯпЖЮ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
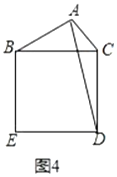
ЁОД№АИЁПЃЈ1ЃЉЂй![]() ЃЌЂк
ЃЌЂк![]() ЃЛЃЈ2ЃЉЯъМћНтЮіЃЛЃЈ3ЃЉ
ЃЛЃЈ2ЃЉЯъМћНтЮіЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉбгГЄ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() .вРОн
.вРОн![]() жЄУї
жЄУї![]() ЃЌгЩШЋЕШШ§НЧаЮЕФаджЪПЩЕУЕН
ЃЌгЩШЋЕШШ§НЧаЮЕФаджЪПЩЕУЕН![]() ЃЌШЛКѓдйгЩ
ЃЌШЛКѓдйгЩ![]() ЃЌ
ЃЌ![]() ЃЌПЩЕУЕН
ЃЌПЩЕУЕН![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ2ЫљЪОЃКМЧ![]() гы
гы![]() ЕФНЛЕуЮЊ
ЕФНЛЕуЮЊ![]() ЃЌ
ЃЌ![]() гы
гы![]() ЕФНЛЕуЮЊ
ЕФНЛЕуЮЊ![]() .ЯШжЄУї
.ЯШжЄУї![]() ЃЌШЛКѓвРОн
ЃЌШЛКѓвРОн![]() жЄУї
жЄУї![]() ЃЌгЩШЋЕШШ§НЧаЮЕФаджЪПЩЕУЕН
ЃЌгЩШЋЕШШ§НЧаЮЕФаджЪПЩЕУЕН![]() ЃЌШЛКѓгЩ
ЃЌШЛКѓгЩ![]() ЃЌ
ЃЌ![]() ЃЌПЩжЄУї
ЃЌПЩжЄУї![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЙ§Еу![]() зї
зї![]() ЃЌШЁ
ЃЌШЁ![]() ЃЌСЌНс
ЃЌСЌНс![]() ЃЌЯШдкЕШбќжБНЧ
ЃЌЯШдкЕШбќжБНЧ![]() жаЧѓЕУ
жаЧѓЕУ![]() ЕФГЄЃЌШЛКѓвРОнШ§НЧаЮЕФШ§БпЙиЯЕПЩЧѓЕУ
ЕФГЄЃЌШЛКѓвРОнШ§НЧаЮЕФШ§БпЙиЯЕПЩЧѓЕУ![]() ЕФШЁжЕЗЖЮЇЃЌзюКѓвРОн
ЕФШЁжЕЗЖЮЇЃЌзюКѓвРОн![]() жЄУї
жЄУї![]() ЃЌгЩШЋЕШШ§НЧаЮЕФаджЪЕУЕН
ЃЌгЩШЋЕШШ§НЧаЮЕФаджЪЕУЕН![]() ЃЌЙЪДЫПЩЧѓЕУ
ЃЌЙЪДЫПЩЧѓЕУ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
НтЃКЃЈ1ЃЉбгГЄ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() .
.
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ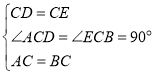 ЃЌ
ЃЌ
Ёр![]() .
.
Ёр![]() ЃЌ
ЃЌ![]() .
.
гжЁп![]() ЃЌ
ЃЌ
Ёр![]() .
.
Ёр![]() .
.
ЙЪД№АИЮЊЃК![]() ЃЌ
ЃЌ![]() .
.
ЃЈ2ЃЉШчЭМ2ЫљЪОЃКМЧ![]() гы
гы![]() ЕФНЛЕуЮЊ
ЕФНЛЕуЮЊ![]() ЃЌ
ЃЌ![]() гы
гы![]() ЕФНЛЕуЮЊ
ЕФНЛЕуЮЊ![]() .
.
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() .
.
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ ЃЌ
ЃЌ
Ёр![]() .
.
Ёр![]() ЃЌ
ЃЌ![]() .
.
гжЁп![]() ЃЌ
ЃЌ
Ёр![]() .
.
Ёр![]() .
.
ЃЈ3ЃЉШчЭМ3ЫљЪОЃКЙ§Еу![]() зї
зї![]() ЃЌШЁ
ЃЌШЁ![]() ЃЌСЌНс
ЃЌСЌНс![]() .
.
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() .
.
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() .
.
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() .
.
дк![]() КЭ
КЭ![]() жа
жа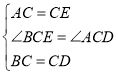 ЃЌ
ЃЌ
Ёр![]() .
.
Ёр![]() .
.
Ёр![]() .
.


 ЬвРюЮФЛЏПьРжЪюМйЮфККГіАцЩчЯЕСаД№АИ
ЬвРюЮФЛЏПьРжЪюМйЮфККГіАцЩчЯЕСаД№АИ гХауЩњПьРжМйЦкУПвЛЬьШЋаТКЎМйзївЕБОЯЕСаД№АИ
гХауЩњПьРжМйЦкУПвЛЬьШЋаТКЎМйзївЕБОЯЕСаД№АИ ЪюМйНгСІШќаТНЎЧрЩйФъГіАцЩчЯЕСаД№АИ
ЪюМйНгСІШќаТНЎЧрЩйФъГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2016ФъФГЯиЭЖШы200ЭђдЊгУгкХЉДхЁАЗіЦЖЙЄГЬЁБЃЌМЦЛЎвдКѓУПФъвдЯрЭЌЕФдіГЄТЪЭЖШыЃЌ2018ФъИУЯиМЦЛЎЭЖШыЁАЗіЦЖЙЄГЬЁБ338ЭђдЊЃЎ
ЃЈ1ЃЉЧѓИУЯиЭЖШыЁАЗіЦЖЙЄГЬЁБЕФФъЦНОљдіГЄТЪЃЎ
ЃЈ2ЃЉДг2016ФъЕН2018ФъЃЌИУЯиШ§ФъЙВЭЖШыЁАЗіЦЖЙЄГЬЁБЖрЩйЭђдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЦћГЕБъжОжаЃЌЪЧжааФЖдГЦЭМаЮЕФЪЧЃЈЁЁЁЁЃЉ
A.  B.
B.  C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
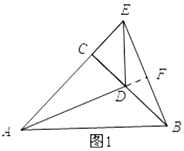
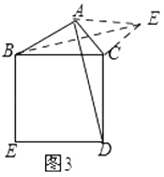
ЁОЬтФПЁПдкСтаЮABCDКЭСтаЮBEFGжаЃЌЕуAЁЂBЁЂGЙВЯпЃЌЕуCдкBEЩЯЃЌЁЯDABЃН60ЁуЃЌAGЃН8ЃЌЕуMЃЌNЗжБ№ЪЧACКЭEGЕФжаЕуЃЌдђMNЕФзюаЁжЕЕШгкЃЈЁЁЁЁЃЉ
A.2![]() B.4C.2
B.4C.2![]() D.6
D.6
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
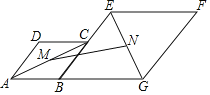
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНЉx2+x+6МАвЛДЮКЏЪ§yЃНЉx+mЃЌНЋИУЖўДЮКЏЪ§дкxжсЩЯЗНЕФЭМЯѓбиxжсЗелЕНxжсЯТЗНЃЌЭМЯѓЕФЦфгрВПЗжВЛБфЃЌЕУЕНвЛИіаТКЏЪ§ЃЈШчЭМЫљЪОЃЉЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§yЃНЉx2+x+6ЕФЖЅЕузјБъКЭxжсЕФНЛЕузјБъЃЛ
ЃЈ2ЃЉжБНгаДГіаТКЏЪ§ЖдгІЕФНтЮіЪНЃЛ
ЃЈ3ЃЉЕБжБЯпyЃНЉx+mгыаТЭМЯѓгаЫФИіНЛЕуЪБЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕШБпЁїOA1B1ЃЌЖЅЕуA1дкЫЋЧњЯпy=![]() ЃЈxЃО0ЃЉЩЯЃЌЕуB1ЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЎЙ§B1зїB1A2ЁЮOA1НЛЫЋЧњЯпгкЕуA2ЃЌЙ§A2зїA2B2ЁЮA1B1НЛxжсгкЕуB2ЃЌЕУЕНЕкЖўИіЕШБпЁїB1A2B2ЃЛЙ§B2зїB2A3ЁЮB1A2НЛЫЋЧњЯпгкЕуA3ЃЌЙ§A3зїA3B3ЁЮA2B2НЛxжсгкЕуB3ЃЌЕУЕНЕкШ§ИіЕШБпЁїB2A3B3ЃЛвдДЫРрЭЦЃЌЁЃЌдђЕуB6ЕФзјБъЮЊ_____ЃЎ
ЃЈxЃО0ЃЉЩЯЃЌЕуB1ЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЎЙ§B1зїB1A2ЁЮOA1НЛЫЋЧњЯпгкЕуA2ЃЌЙ§A2зїA2B2ЁЮA1B1НЛxжсгкЕуB2ЃЌЕУЕНЕкЖўИіЕШБпЁїB1A2B2ЃЛЙ§B2зїB2A3ЁЮB1A2НЛЫЋЧњЯпгкЕуA3ЃЌЙ§A3зїA3B3ЁЮA2B2НЛxжсгкЕуB3ЃЌЕУЕНЕкШ§ИіЕШБпЁїB2A3B3ЃЛвдДЫРрЭЦЃЌЁЃЌдђЕуB6ЕФзјБъЮЊ_____ЃЎ
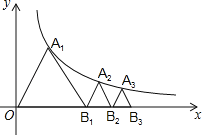
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЗНИёжНжаЕФУПИіаЁЗНИёЖМЪЧБпГЄЮЊ1ИіЕЅЮЛЕФе§ЗНаЮЃЌдкНЈСЂЦНУцжБНЧзјБъЯЕКѓЃЌЁїABCЕФЖЅЕуОљдкИёЕуЩЯЃЌЕуBЕФзјБъЮЊЃЈ1ЃЌ0ЃЉ
ЃЈ1ЃЉЛГіЁїABCЙигкxжсЖдГЦЕФЁїA1B1C1ЃЛ
ЃЈ2ЃЉЛГіНЋЁїABCШЦдЕуOАДФцЪБеыа§зЊ90ЁуЫљЕУЕФЁїA2B2C2ЃЛ
ЃЈ3ЃЉЁїA1B1C1гыЁїA2B2C2ГЩжсЖдГЦЭМаЮТ№ЃПШєГЩжсЖдГЦЭМаЮЃЌЛГіЫљгаЕФЖдГЦжсЃЛ
ЃЈ4ЃЉЁїA1B1C1гыЁїA2B2C2ГЩжааФЖдГЦЭМаЮТ№ЃПШєГЩжааФЖдГЦЭМаЮЃЌаДГіЫљгаЕФЖдГЦжааФЕФзјБъЃЎ
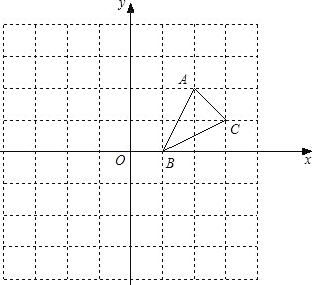
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЭјЕъЯњЪлФГПюЭЏзАЃЌУПМўЪлМл60дЊЃЌУПаЧЦкПЩТє300МўЃЌЮЊСЫДйЯњЃЌИУЭјЕъОіЖЈНЕМлЯњЪлЃЎЪаГЁЕїВщЗДгГЃКУПНЕМл1дЊЃЌУПаЧЦкПЩЖрТє30МўЃЎвбжЊИУПюЭЏзАУПМўГЩБОМл40дЊЃЌЩшИУПюЭЏзАУПМўЪлМлxдЊЃЌУПаЧЦкЕФЯњЪлСПЮЊyМўЃЎ
ЃЈ1ЃЉЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЕБУПМўЪлМлЖЈЮЊЖрЩйдЊЪБЃЌУПаЧЦкЕФЯњЪлРћШѓзюДѓЃЌзюДѓРћШѓЖрЩйдЊЃП
ЃЈ3ЃЉШєИУЭјЕъУПаЧЦкЯывЊЛёЕУВЛЕЭгк6480дЊЕФРћШѓЃЌУПаЧЦкжСЩйвЊЯњЪлИУПюЭЏзАЖрЩйМўЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЛѕГЕЯњЪлЙЋЫОЃЌЗжБ№ЪдЯњЪлСНжжаЭКХЛѕГЕИївЛИідТЃЌВЂДгжабЁдёвЛжжГЄЦкЯњЪлЃЌЩшУПдТЯњЪлСПЮЊxСОШєЯњЪлМзаЭЛѕГЕЃЌУПдТЯњЪлЕФРћШѓЮЊy1(ЭђдЊ)ЃЌвбжЊУПСОМзаЭЛѕГЕЕФРћШѓЮЊ(m+6)ЭђдЊЃЌ(mЪЧГЃЪ§ЃЌ9ЁмmЁм11)ЃЌУПдТЛЙашжЇГіЦфЫћЗбгУ8ЭђдЊЃЌЪмЬѕМўЯожЦУПдТзюЖрФмЯњЪлМзаЭЛѕГЕ25СОЃЛШєЯњЪлвваЭЛѕГЕЃЌУПдТЕФРћШѓy2(ЭђдЊ)гыxЕФКЏЪ§ЙиЯЕЪНЮЊy2=ax2+bx-25ЃЌЧвЕБxЃН10ЪБЃЌy2ЃН20ЃЌЕБxЃН20ЪБЃЌy2ЃН55ЃЌЪмЬѕМўЯожЦУПдТзюЖрФмЯњЪлвваЭЛѕГЕ40СОЃЎ
(1)ЗжБ№ЧѓГіy1ЁЂy2гыxЕФКЏЪ§ЙиЯЕЪНЃЌВЂШЗЖЈxЕФШЁжЕЗЖЗЖЮЇЃЛ
(2)ЗжБ№ЧѓГіЯњЪлетСНжжЛѕГЕЕФзюДѓдТРћШѓЃЛ(зюДѓРћШѓФмЧѓжЕЕФЧѓжЕЃЌВЛФмЧѓжЕЕФгУЪНзгБэЪО)
(3)ЮЊЛёЕУзюДѓдТРћШѓЃЌИУЙЋЫОгІИУбЁдёЯњЪлФФжжЛѕГЕЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com