
【题目】某校课外兴趣小组在本校学生中开展“感动中国2013年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别 | A | B | C | D |
频数 | 30 | 40 | 24 | b |
频率 | a | 0.4 | 0.24 | 0.06 |
(1)表中的a= , b=;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数; 
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
【题目】如图,OA=2,以点A为圆心,1为半径画⊙A与OA的延长线交于点C,过点A画OA的垂线,垂线与⊙A的一个交点为B,连接BC 
(1)线段BC的长等于;
(2)请在图中按下列要求逐一操作,并回答问题: 以点为圆心,以线段的长为半径画弧,与射线BA交于点D,使线段OD的长等于 ![]()
(3)连OD,在OD上画出点P,使OP的长等于 ![]() ,请写出画法,并说明理由.
,请写出画法,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知过点(2,﹣3)的直线y=ax+b(a≠0)不经过第一象限,设s=a+2b,则s的取值范围是( )
A.﹣5≤s≤﹣ ![]()
B.﹣6<s≤﹣ ![]()
C.﹣6≤s≤﹣ ![]()
D.﹣7<s≤﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.
(1)如图1,已知折痕与边BC交于点O,连结AP、OP、OA. ①求证:△OCP∽△PDA;
②若△OCP与△PDA的面积比为1:4,求边AB的长;
(2)若图1中的点P恰好是CD边的中点,求∠OAB的度数;
(3)如图2, ![]()
![]()
![]()
![]()
![]()
![]() ,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.
,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度. 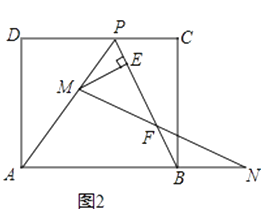
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=36°,

(1)作出AB边的垂直平分线DE,交AC于点D,交AB于点E,连接BD;
(2)下列结论正确的是:
① BD平分∠ABC;② AD=BD=BC;③ △BDC的周长等于AB+BC; ④ D点是AC中点;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点A出发,沿射线AD移动,以CE为直径作圆O,点F为圆O与射线BD的公共点,连接EF、CF,过点E作EG⊥EF,EG与圆O相交于点G,连接CG. 
(1)试说明四边形EFCG是矩形;
(2)当圆O与射线BD相切时,点E停止移动,在点E移动的过程中, ①矩形EFCG的面积是否存在最大值或最小值?若存在,求出这个最大值或最小值;若不存在,说明理由;
②求点G移动路线的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=8cm.BC=4cm,CD=5cm.动点P从点B开始沿折线BC﹣CD﹣DA以1cm/s的速度运动到点A.设点P运动的时间为t(s),△PAB面积为S(cm2). 
(1)当t=2时,求S的值;
(2)当点P在边DA上运动时,求S关于t的函数表达式;
(3)当S=12时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,自来水厂A和村庄B在小河l的两侧,现要在A,B间铺设一条输水管道.为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q处,测得A位于北偏西49°方向,B位于南偏西41°方向.
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A,B间的距离.(参考数据cos41°≈0.75)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com