
【题目】
(1)计算:(3.14﹣π)0+(﹣ ![]() )﹣2﹣2sin30°;
)﹣2﹣2sin30°;
(2)化简: ![]() ﹣
﹣ ![]() ÷
÷ ![]() .
.
【答案】
(1)解:原式=1+4﹣1=4;
(2)解:原式= ![]() ﹣
﹣ ![]()
![]() =
= ![]() ﹣
﹣ ![]() =
= ![]() .
.
【解析】(1)原式第一项利用零指数幂法则计算,第二项利用负指数幂法则计算,最后一项利用特殊角的三角函数值计算即可得到结果;(2)原式第二项利用除法法则变形,约分后两项利用同分母分式的减法法则计算即可得到结果.
【考点精析】本题主要考查了分式的混合运算和零指数幂法则的相关知识点,需要掌握运算的顺序:第一级运算是加法和减法;第二级运算是乘法和除法;第三级运算是乘方.如果一个式子里含有几级运算,那么先做第三级运算,再作第二级运算,最后再做第一级运算;如果有括号先做括号里面的运算.如顺口溜:"先三后二再做一,有了括号先做里."当有多层括号时,先算括号内的运算,从里向外{[(?)]};零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数)才能正确解答此题.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
【题目】我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线y= ![]() 的一部分,请根据图中信息解答下列问题:
的一部分,请根据图中信息解答下列问题: 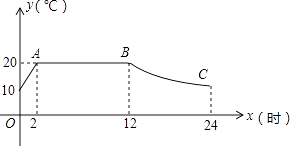
(1)求k的值;
(2)恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y1=kx+m(k≠0)和二次函数y2=ax2+bx+c(a≠0)的自变量和对应函数值如表:
x | … | ﹣1 | 0 | 2 | 4 | … |
y1 | … | 0 | 1 | 3 | 5 | … |
x | … | ﹣1 | 1 | 3 | 4 | … |
y2 | … | 0 | ﹣4 | 0 | 5 | … |
当y2>y1时,自变量x的取值范围是( )
A.x<﹣1
B.x>4
C.﹣1<x<4
D.x<﹣1或x>4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解“通话时长”(“通话时长”指每次通话时间)的分布情况,小强收集了他家1000个“通话时长”数据,这些数据均不超过18(分钟).他从中随机抽取了若干个数据作为样本,统计结果如下表,并绘制了不完整的频数分布直方图. 
“通话时长” | 0<x≤3 | 3<x≤6 | 6<x≤9 | 9<x≤12 | 12<x≤15 | 15<x≤18 |
次数 | 36 | a | 8 | 12 | 8 | 12 |
根据表、图提供的信息,解答下面的问题:
(1)a= , 样本容量是;
(2)求样本中“通话时长”不超过9分钟的频率:;
(3)请估计小强家这1000次通话中“通话时长”超过15分钟的次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道平行四边形那有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论
(1)【发现与证明】
在ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′D.
结论1:B′D∥AC;
结论2:△AB′C与ABCD重叠部分的图形是等腰三角形.
…
请利用图1证明结论1或结论2.
(2)【应用与探究】
在ABCD中,∠B=30°,将△ABC沿AC翻折至△AB′C,连接B′D.
如图1,若AB= ![]() ,∠AB′D=75°,则∠ACB= , BC=;
,∠AB′D=75°,则∠ACB= , BC=;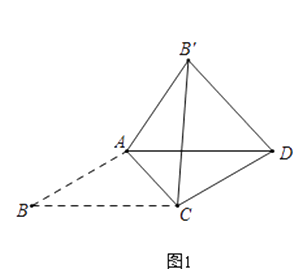
(3)如图2,AB=2 ![]() ,BC=1,AB′与CD相交于点E,求△AEC的面积;
,BC=1,AB′与CD相交于点E,求△AEC的面积;
(4)已知AB=2 ![]() ,当BC的长为多少时,△AB′D是直角三角形?
,当BC的长为多少时,△AB′D是直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算T,规定:T(x,y)= ![]() (其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=
(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)= ![]() =b.
=b.
(1)已知T(1,﹣1)=﹣2,T(4,2)=1. ①求a,b的值;
②若关于m的不等式组 ![]() 恰好有3个整数解,求实数p的取值范围;
恰好有3个整数解,求实数p的取值范围;
(2)若T(x,y)=T(y,x)对任意实数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b应满足怎样的关系式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校课外兴趣小组在本校学生中开展“感动中国2013年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别 | A | B | C | D |
频数 | 30 | 40 | 24 | b |
频率 | a | 0.4 | 0.24 | 0.06 |
(1)表中的a= , b=;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数; 
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在5次打靶测试中命中的环数如下: 甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | 8 | 0.4 | |
乙 | 9 | 3.2 |
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 . (填“变大”、“变小”或“不变”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF. 
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com