
����Ŀ������֪��ƽ���ı������кܶ����ʣ�����������ǰ�ƽ���ı�����������һ���Խ��߷��ۣ��ᷢ�������л��и���Ľ���
��1����������֤����
��ABCD��AB��BC������ABC��AC��������AB��C������B��D��
����1��B��D��AC��
����2����AB��C��ABCD�ص����ֵ�ͼ���ǵ��������Σ�
��
������ͼ1֤������1�����2��
��2����Ӧ����̽����
��ABCD�У���B=30�㣬����ABC��AC��������AB��C������B��D��
��ͼ1����AB= ![]() ����AB��D=75�㣬���ACB= �� BC=��
����AB��D=75�㣬���ACB= �� BC=��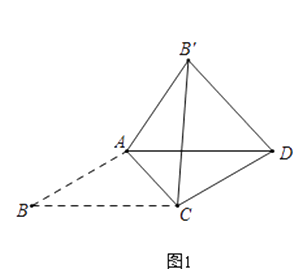
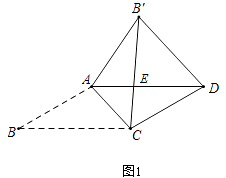
��3����ͼ2��AB=2 ![]() ��BC=1��AB����CD�ཻ�ڵ�E�����AEC�������
��BC=1��AB����CD�ཻ�ڵ�E�����AEC�������
��4����֪AB=2 ![]() ����BC�ij�Ϊ����ʱ����AB��D��ֱ�������Σ�
����BC�ij�Ϊ����ʱ����AB��D��ֱ�������Σ�
���𰸡�
��1��
��ABCD��AB��BC������ABC��AC��������AB��C������B��D��
��ͼ1�����ı���ABCD��ƽ���ı��Σ�
��AB=CD��BC=AD����B=��ADC��
�߽���ABC��AC��������AB��C��
��AB��=AB��B��C=BC����AB��C=��B��
��AB��=CD��B��C=AD����AB��C=��ADC��
�ڡ�AB��C�͡�CAD�У�
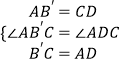 ��
��
���AB��C�ա�CAD��SAS����
���ACB��=��CAD��
��AD��B��C�ཻ��E��
��AE=CE��
���ACE�ǵ��������Σ�
����AB��C��ABCD�ص����ֵ�ͼ���ǵ��������Σ�
��B��C=AD��AE=CE��
��B��E=DE��
���CB��D=��ADB�䣬
�ߡ�AEC=��B��ED����ACB��=��CAD��
���ADB��=��DAC��
��B��D��AC��
��2��45�㣻![]()
��3��
�⣺��ͼ2��

��CG��AB����G��
�ߡ�B=30�㣬
���AB��C=30�㣬
��CG= ![]() B��C=
B��C= ![]() BC=
BC= ![]() ��B��G=
��B��G= ![]() B��C=
B��C= ![]() BC=
BC= ![]() ��
��
��AB��=AB=2 ![]() ��
��
��AG=2 ![]() ��
�� ![]() =
= ![]() ��
��
��AE=CE=x����EG= ![]() ��x��
��x��
��CG2+EG2=CE2��
�ࣨ ![]() ��2+��
��2+�� ![]() ��x��2=x2�����x=
��x��2=x2�����x= ![]() ��
��
��AE= ![]() ��
��
���AEC�����= ![]() AECG=
AECG= ![]() ��
�� ![]() ��
�� ![]() =
= ![]() ��
��
��4��
�⣺��ͼ2����AD=BC��BC=B��C��
��AD=B��C��
��AC��B��D��
���ı���ACB��D�ǵ������Σ�
�ߡ�B=30�㣬
���AB��C=��CDA=30�㣬
�ߡ�AB��D��ֱ�������Σ�
����B��AD=90�㣬AB��BCʱ��
���ADB��=��CB��D=y��
���AB��D=y��30�㣬
�ߡ�AB��D+��ADB��=90�㣬
��y��30��+y=90�㣬���y=60�㣬
���AB��D=y��30��=30�㣬
��AB��=AB=2 ![]() ��
��
��AD= ![]() ��2
��2 ![]() =2��
=2��
��BC=2��
����ADB��=90�㣬AB��BCʱ����ͼ3��

��AD=BC��BC=B��C��
��AD=B��C��
��AC��B��D��
���ı���ACB��D�ǵ������Σ�
�ߡ�ADB��=90�㣬
���ı���ACB��D�Ǿ��Σ�
���ACB��=90�㣬
���ACB=90�㣬
�ߡ�B=30�㣬AB=2 ![]() ��
��
��BC= ![]() AB=
AB= ![]() ��2
��2 ![]() =3��
=3��
����B��AD=90��AB��BCʱ����ͼ4��

��AD=BC��BC=B��C��
��AD=B��C��
��AC��B��D����B��AD=90�㣬
���B��GC=90�㣬
�ߡ�B=30�㣬AB=2 ![]() ��
��
���AB��C=30�㣬
��GC= ![]() B��C=
B��C= ![]() BC��
BC��
��G��BC���е㣬
��RT��ABG��BG= ![]() AB=
AB= ![]() ��2
��2 ![]() =3��
=3��
��BC=6��
����AB��D=90��ʱ����ͼ5��

��AD=BC��BC=B��C��
��AD=B��C��
��AC��B��D��
���ı���ACDB���ǵ������Σ�
�ߡ�AB��D=90�㣬
���ı���ACDB���Ǿ��Σ�
���BAC=90�㣬
�ߡ�B=30�㣬AB=2 ![]() ��
��
��BC=AB�� ![]() =2
=2 ![]() ��
�� ![]() =4��
=4��
����֪��BC�ij�Ϊ2��3��4��6ʱ����AB��D��ֱ�������Σ�
����������������֤����ͨ��������ȫ�ȼ�����á�ACB��=��CAD�����ɵõ�����2���������ݵ��������ε�����֤�á�ADB��=��DAC������ƽ���ߵ��ж�����֤�ý���1����Ӧ����̽������1�����ݶ��۵�������á�AB��C=30�㣬�Ӷ���á�CB��D=45�㣬����B��D��AC���ó���ACB��=��CB��D=45�㣬����������á�ACB=45�㣻��AG��BC��G�����ݽ�ֱ�������μ������BC����2����CG��AB����G��ͨ����ֱ�����������CG= ![]() ��B��G=
��B��G= ![]() ���������AG=2
���������AG=2 ![]() ��
�� ![]() =
= ![]() ����AE=CE=x����EG=
����AE=CE=x����EG= ![]() ��x�����ݹ��ɶ����������xֵ����AE��ֵ��Ȼ����������ε������ʽ������á�AEC���������3����֤���ı���ACB��D�ǵ������Σ����ݵ������ε����ʵó���AB��C=��CDA=30�㣬��B��AD=��DCB��=90�㣬���ADB��=��CB��D=y�����AB��D=y��30�㣬���ݡ�AB��D+��ADB��=90�㣬�ó�y��30��+y=90�㣬���y=60�㣬������á�AB��D=30�㣬ͨ����ֱ�������μ������BC��
��x�����ݹ��ɶ����������xֵ����AE��ֵ��Ȼ����������ε������ʽ������á�AEC���������3����֤���ı���ACB��D�ǵ������Σ����ݵ������ε����ʵó���AB��C=��CDA=30�㣬��B��AD=��DCB��=90�㣬���ADB��=��CB��D=y�����AB��D=y��30�㣬���ݡ�AB��D+��ADB��=90�㣬�ó�y��30��+y=90�㣬���y=60�㣬������á�AB��D=30�㣬ͨ����ֱ�������μ������BC��
��Ӧ����̽������1����ͼ1������ABCD�У���B=30�㣬����ABC��AC��������AB��C��
���AB��C=30�㣬
�ߡ�AB��D=75�㣬
���CB��D=45�㣬
��B��D��AC��
���ACB��=��CB��D=45�㣬
�ߡ�ACB=��ACB�䣬
���ACB=45�㣻
��AG��BC��G��
��AG=CG��
�ߡ�B=30�㣬
��AG= ![]() AB=
AB= ![]()
![]() =
= ![]() ��
��
��CG= ![]() ��BG=
��BG= ![]() =
= ![]() ��
��
��BC=BG+CG= ![]() ��
��
���Դ��ǣ�45�㣬 ![]() ��
��
�����㾫����������Ҫ������ƽ���ı��ε��ж������֪ʶ�㣬��Ҫ��������Ա߷ֱ�ƽ�е��ı�����ƽ���ı��Σ�����Ա߷ֱ���ȵ��ı�����ƽ���ı��Σ�һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ�����ԽǷֱ���ȵ��ı�����ƽ���ı��Σ��Խ�����ƽ�ֵ��ı�����ƽ���ı��β�����ȷ�����⣮


 ����С����ͬ������ϵ�д�
����С����ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����λͬѧ�μ���ѧ�ۺ����ʲ��ԣ�����ɼ����£���λ���֣�
������� | �ռ���ͼ�� | ͳ������� | �ۺ���ʵ�� | |
ѧ���� | 90 | 93 | 89 | 90 |
ѧ���� | 94 | 92 | 94 | 86 |
��1���ֱ����ס��ҳɼ�����λ����
��2���������������ռ���ͼ�Ρ�ͳ������ʡ��ۺ���ʵ���ijɼ���3��3��2��2���㣬��ô�ס��ҵ���ѧ�ۺ����ʳɼ��ֱ�Ϊ���ٷ֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�ı�AB�ӳ�����E��ʹBE=AB������DE������BC�ڵ�F�� 
��1����֤����BEF�ա�CDF��
��2������BD��CE������BFD=2��A����֤���ı���BECD�Ǿ��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���㣨2����3����ֱ��y=ax+b��a��0����������һ���ޣ���s=a+2b����s��ȡֵ��Χ�ǣ� ��
A.��5��s�ܩ� ![]()
B.��6��s�ܩ� ![]()
C.��6��s�ܩ� ![]()
D.��7��s�ܩ� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�ֱ��y=kx+4��k��0����y�ύ�ڵ�A��
��1����ͼ��ֱ��y=��2x+1��ֱ��y=kx+4��k��0�����ڵ�B����y�ύ�ڵ�C����B�ĺ�����Ϊ��1�� �����B�����꼰k��ֵ��
��ֱ��y=��2x+1��ֱ��y=kx+4��y����Χ�ɵġ�ABC�����������
��2��ֱ��y=kx+4��k��0����x�ύ�ڵ�E��x0 �� 0��������2��x0����1����k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
��1�����㣺��3.14���У�0+���� ![]() ����2��2sin30�㣻
����2��2sin30�㣻
��2������ ![]() ��
�� ![]() ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABCD��һ����AD=8��������ABCD�۵���ʹ�ö���B����CD���ϵ�P�㴦��
��1����ͼ1����֪�ۺ����BC���ڵ�O������AP��OP��OA�� ����֤����OCP�ס�PDA��
������OCP���PDA�������Ϊ1��4�����AB�ij���
��2����ͼ1�еĵ�Pǡ����CD�ߵ��е㣬���OAB�Ķ�����
��3����ͼ2�� ![]()
![]()
![]()
![]()
![]()
![]() ����ȥ�ۺ�AO���߶�OP������BP������M���߶�AP�ϣ���M���P��A���غϣ�������N���߶�AB���ӳ����ϣ���BN=PM������MN��PB�ڵ�F����ME��BP�ڵ�E�����ʵ���M��N���ƶ������У��߶�EF�ij����Ƿ����仯�����仯��˵�����ɣ������䣬����߶�EF�ij��ȣ�
����ȥ�ۺ�AO���߶�OP������BP������M���߶�AP�ϣ���M���P��A���غϣ�������N���߶�AB���ӳ����ϣ���BN=PM������MN��PB�ڵ�F����ME��BP�ڵ�E�����ʵ���M��N���ƶ������У��߶�EF�ij����Ƿ����仯�����仯��˵�����ɣ������䣬����߶�EF�ij��ȣ� 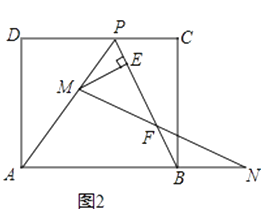
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ı�AB=3cm��AD=4cm����E�ӵ�A������������AD�ƶ�����CEΪֱ����ԲO����FΪԲO������BD�Ĺ����㣬����EF��CF������E��EG��EF��EG��ԲO�ཻ�ڵ�G������CG�� 
��1����˵���ı���EFCG�Ǿ��Σ�
��2����ԲO������BD����ʱ����Eֹͣ�ƶ����ڵ�E�ƶ��Ĺ����У� �پ���EFCG������Ƿ�������ֵ����Сֵ�������ڣ����������ֵ����Сֵ���������ڣ�˵�����ɣ�
�����G�ƶ�·�ߵij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ۿ�A�ڹ۲�վO����������OA=4km��ij���Ӹۿ�A�������ر�ƫ��15�㷽����һ�ξ����B������ʱ�ӹ۲�վO����øô�λ�ڱ�ƫ��60��ķ�����ô����еľ��루��AB�ij���Ϊ�� ��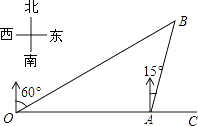
A.4km
B.2 ![]() km
km
C.2 ![]() km
km
D.�� ![]() +1��km
+1��km
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com