
【题目】甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数 | 空间与图形 | 统计与概率 | 综合与实践 | |
学生甲 | 90 | 93 | 89 | 90 |
学生乙 | 94 | 92 | 94 | 86 |
(1)分别计算甲、乙成绩的中位数;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分?
【答案】
(1)解:甲的成绩从小到大的顺序排列为:89,90,90,93,中位数为90;
乙的成绩从小到大的顺序排列为:86,92,94,94,中位数为(92+94)÷2=93.
答:甲成绩的中位数是90,乙成绩的中位数是93
(2)解:3+3+2+2=10
甲90× ![]() +93×
+93× ![]() +89×
+89× ![]() +90×
+90× ![]()
=27+27.9+17.8+18
=90.7(分)
乙94× ![]() +92×
+92× ![]() +94×
+94× ![]() +86×
+86× ![]()
=28.2+27.6+18.8+17.2
=91.8(分)
答:甲的数学综合素质成绩为90.7分,乙的数学综合素质成绩为91.8分
【解析】(1)将一组数据按照从小到大(或从大到小)的顺序排列,处于中间位置的数就是这组数据的中位数进行分析;(2)数学综合素质成绩=数与代数成绩× ![]() +空间与图形成绩×
+空间与图形成绩× ![]() +统计与概率成绩×
+统计与概率成绩× ![]() +综合与实践成绩×
+综合与实践成绩× ![]() ,依此分别进行计算即可求解.
,依此分别进行计算即可求解.


科目:初中数学 来源: 题型:
【题目】小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍.小颖在小亮出发后50min 才乘上缆车,缆车的平均速度为180m/min.设小亮出发x min后行走的路程为y m,图中的折线表示小亮在整个行走过程中y与x的函数关系. 
(1)小亮行走的总路程是m,他途中休息了min;
(2)①当50≤x≤80时,求y与x的函数关系式; ②当小颖到达缆车终点时,小亮离缆车终点的路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现如今,通过微信朋友圈发布自己每天行走的步数,已成为一种时尚,“健身达人”小张为了了解他的微信朋友圈里大家的运动情况,随机抽取了部分好友进行调查,把他们6月9日那天每天行走的步数情况分为五个类别:A(0﹣4000步)(说明:“0﹣4000”表示大于等于0,小于等于4000,下同),B(4001﹣8000步),C(8001﹣12000步),D(12001﹣16000步),E(16001步及以上),并将统计结果绘制了如图1的图2两幅不完整的统计图. 
请你根据图中提供的信息解答下列问题:
(1)将图1的条形统计图补充完整;
(2)已知小张的微信朋友圈里共500人,请根据本次抽查的结果,估计在他的微信朋友圈里6月9日那天行走不超过8000步的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点F在平行四边形ABCD的边AB上,射线CF交DA的延长线于点E,在不添加辅助线的情况下,与△AEF相似的三角形有( ) 
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线y= ![]() 的一部分,请根据图中信息解答下列问题:
的一部分,请根据图中信息解答下列问题: 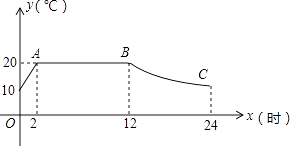
(1)求k的值;
(2)恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( ) 
A.![]()
B.2 ![]()
C.3
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,地面上两个村庄C、D处于同一水平线上,一飞行器在空中以6千米/小时的速度沿MN方向水平飞行,航线MN与C、D在同一铅直平面内.当该飞行器飞行至村庄C的正上方A处时,测得∠NAD=60°;该飞行器从A处飞行40分钟至B处时,测得∠ABD=75°.求村庄C、D间的距离( ![]() 取1.73,结果精确到0.1千米)
取1.73,结果精确到0.1千米) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道平行四边形那有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论
(1)【发现与证明】
在ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′D.
结论1:B′D∥AC;
结论2:△AB′C与ABCD重叠部分的图形是等腰三角形.
…
请利用图1证明结论1或结论2.
(2)【应用与探究】
在ABCD中,∠B=30°,将△ABC沿AC翻折至△AB′C,连接B′D.
如图1,若AB= ![]() ,∠AB′D=75°,则∠ACB= , BC=;
,∠AB′D=75°,则∠ACB= , BC=;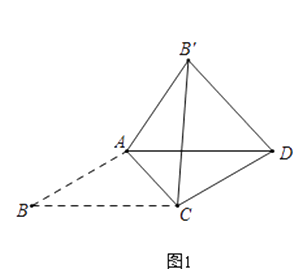
(3)如图2,AB=2 ![]() ,BC=1,AB′与CD相交于点E,求△AEC的面积;
,BC=1,AB′与CD相交于点E,求△AEC的面积;
(4)已知AB=2 ![]() ,当BC的长为多少时,△AB′D是直角三角形?
,当BC的长为多少时,△AB′D是直角三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com