
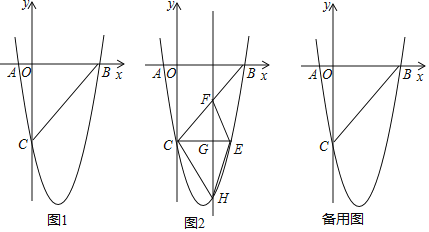
【题目】如图1,在平面直角坐标系中,已知抛物线y=ax2+bx﹣5与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C.
(1)求抛物线的函数表达式;
(2)如图2,CE∥x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别相交于点F,G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标;
(3)若点K为抛物线的顶点,点M(4,m)是该抛物线上的一点,在x轴,y轴上分别找点P,Q,使四边形PQKM的周长最小,求出点P,Q的坐标.
【答案】(1)y=x2﹣4x﹣5;(2)H(![]() ,﹣
,﹣![]() );(3)P(
);(3)P(![]() ,0),Q(0,﹣
,0),Q(0,﹣![]() )
)
【解析】
(1)根据待定系数法直接确定出抛物线解析式;
(2)先求出直线BC的解析式,进而求出四边形CHEF的面积的函数关系式,即可求出;
(3)利用对称性找出点P,Q的位置,进而求出P,Q的坐标.
(1)∵点A(﹣1,0),B(5,0)在抛物线y=ax2+bx﹣5上,
∴![]() ,
,
解得![]() ,
,
∴抛物线的表达式为y=x2﹣4x﹣5,
(2)设H(t,t2﹣4t﹣5),
∵CE∥x轴,
∴点E的纵坐标为﹣5,
∵E在抛物线上,
∴x2﹣4x﹣5=﹣5,
∴x=0(舍)或x=4,
∴E(4,﹣5),
∴CE=4,
∵B(5,0),C(0,﹣5),
∴直线BC的解析式为y=x﹣5,
∴F(t,t﹣5),
∴HF=t﹣5﹣(t2﹣4t﹣5)=﹣(t﹣![]() )2+
)2+![]() ,
,
∵CE∥x轴,HF∥y轴,
∴CE⊥HF,
∴S四边形CHEF=![]() CEHF=﹣2(t﹣
CEHF=﹣2(t﹣![]() )2+
)2+![]() ,
,
∴H(![]() ,﹣
,﹣![]() );
);
(3)如图2,
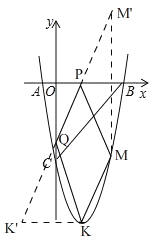
∵K为抛物线的顶点,
∴K(2,﹣9),
∴K关于y轴的对称点K'(﹣2,﹣9),
∵M(4,m)在抛物线上,
∴M(4,﹣5),
∴点M关于x轴的对称点M'(4,5),
∴直线K'M'的解析式为y=![]() ,
,
∴P(![]() ,0),Q(0,﹣
,0),Q(0,﹣![]() ).
).


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
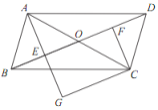
【题目】如图,在□ABCD 中,对角线 AC 与 BD 相交于点 O ,点 E , F 分别为 OB , OD 的中点,延长 AE 至 G ,使 EG =AE ,连接 CG .
(1)求证: △ABE≌△CDF ;
(2)当 AB 与 AC 满足什么数量关系时,四边形 EGCF 是矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
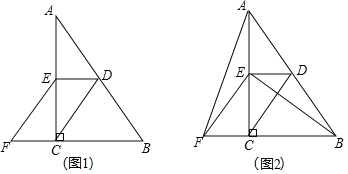
【题目】已知:如图,在![]() 中,
中,![]() ,点D、E分别是AB、AC的中点,点F在BC延长线上,连接EF,且
,点D、E分别是AB、AC的中点,点F在BC延长线上,连接EF,且![]() .
.
![]() 如图1,求证:四边形CDEF是平行四边形;
如图1,求证:四边形CDEF是平行四边形;
![]() 如图2,连接AF、BE,在不添加任何辅助线的情况下,请直接写出图2中所有与
如图2,连接AF、BE,在不添加任何辅助线的情况下,请直接写出图2中所有与![]() 面积相等的三角形.
面积相等的三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°.小聪同学利用直尺和圆规完成了如下作图:
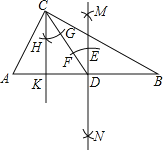
①分别以点A,B为圆心,以大于![]() AB长为半径画弧,两弧交于点M,N,过点M,N作直线与AB交于点D;
AB长为半径画弧,两弧交于点M,N,过点M,N作直线与AB交于点D;
②连接CD,以点D为圆心,以一定长为半径画弧,交MN于点E,交CD于点F,以点C为圆心,以同样定长为半径画弧,与CD交于点G,以点G为圆心,以EF长为半径画弧与前弧交于点H.作射线CH与AB交于点K,请根据以上操作,解答下列问题
(1)由尺规作图可知:直线MN是线段AB的 线,∠DCK= .
(2)若CD=5,AK=2,求CK的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四条直线l1:y1=![]() x,l2:y2=
x,l2:y2=![]() x,l3:y3=﹣
x,l3:y3=﹣![]() x,l4:y4=﹣
x,l4:y4=﹣![]() x,OA1=1,过点A1作A1A2⊥x轴交l1于点A2,再过点A2作A2A3⊥l1,交l2于点A3,再过点A3作A3A4⊥l2交y轴于点A4,……,则点A2020的坐标为_____.
x,OA1=1,过点A1作A1A2⊥x轴交l1于点A2,再过点A2作A2A3⊥l1,交l2于点A3,再过点A3作A3A4⊥l2交y轴于点A4,……,则点A2020的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
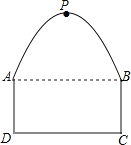
【题目】一座隧道的截面由抛物线和长方形的构成,长方形的长为8米,宽为2米,隧道的最高点P位于AB的中央且距地面6m.
(1)建立适当的直角坐标系,求抛物线解析式;
(2)如果隧道为单行道,一辆货车高4米,宽3米,能否从隧道内通过,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学综合实践活动中,小明计划测量城门大楼的高度,在点B处测得楼顶A的仰角为22°,他正对着城楼前进21米到达C处,再登上3米高的楼台D处,并测得此时楼顶A的仰角为45°.
(1)求城门大楼的高度;
(2)每逢重大节日,城门大楼管理处都要在A,B之间拉上绳子,并在绳子上挂一些彩旗,请你求出A,B之间所挂彩旗的长度(结果保留整数).(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两运动员在长为100m的直道AB(A,B为直道两端点)上进行匀速往返跑训练,两人同时从A点起跑,到达B点后,立即转身跑向A点,到达A点后,又立即转身跑向B点,若甲跑步的速度为5m/s,乙跑步的速度为4m/s,则起跑后2分钟内,两人相遇的次数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于点O,则下列判断不正确的是( )
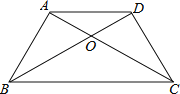
A. △ABC≌△DCBB. △AOD≌△COBC. △ABO≌△DCOD. △ADB≌△DAC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com