
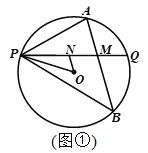
【题目】已知P是⊙O上一点,过点P作不过圆心的弦PQ,在劣弧PQ和优弧PQ上分别有动点A、B(不与P,Q重合),连接AP、BP. 若∠APQ=∠BPQ.
(1)如图1,当∠APQ=45°,AP=1,BP=2![]() 时,求⊙O的半径;
时,求⊙O的半径;
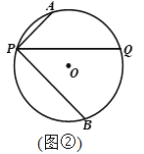
(2)如图2,选接AB,交PQ于点M,点N在线段PM上(不与P、M重合),连接ON、OP,若∠NOP+2∠OPN=90°,探究直线AB与ON的位置关系,并证明.
科目:初中数学 来源: 题型:
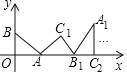
【题目】如图,在平面直角坐标系中,将△ABO沿x轴向右滚动到△AB1C1的位置,再到△A1B1C2的位置……依次进行下去,若已知点A(4,0),B(0,3),则点C100的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1表示的是某手机商店2018年7~12月各月销售总额的统计图,如图2表示的是该商店“华为品牌”手机各月占商店销售总额的百分比统计图。已知7月份“华为品牌”手机的月销售额为12万元,观察如图1、如图2,解析下列问题:
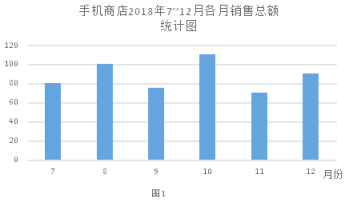
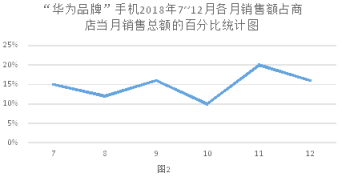
(1)求该手机商店7月份的销售总额。
(2)小明观察图2认为,12月份“华为品牌”手机的销售额比11月份减少了。你同意他的看法吗?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+3x+m-1=0的两个实数根分别为x1,x2.
(1)求m的取值范围.
(2)若2(x1+x2)+ x1x2+10=0.求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1﹣t)(t>0),点P在以D(3,5)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是______________.
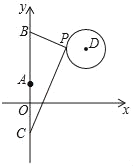
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21,动点P从点D出发,沿射线DA的方向以每秒2个单位长度的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长度的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
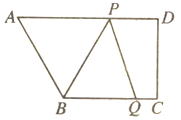
(1)设△BPQ的面积为S,求S与t之间的函数关系式;
(2)当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次羽毛球赛中,甲运动员在离地面![]() 米的P点处发球,球的运动轨迹PAN看作一个抛物线的一部分,当球运动到最高点A时,其高度为3米,离甲运动员站立地点O的水平距离为5米,球网BC离点O的水平距离为6米,以点O为原点建立如图所示的坐标系,乙运动员站立地点M的坐标为(m,0).
米的P点处发球,球的运动轨迹PAN看作一个抛物线的一部分,当球运动到最高点A时,其高度为3米,离甲运动员站立地点O的水平距离为5米,球网BC离点O的水平距离为6米,以点O为原点建立如图所示的坐标系,乙运动员站立地点M的坐标为(m,0).
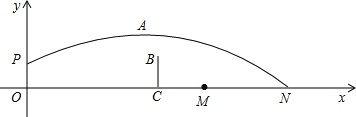
(1)求抛物线的解析式(不要求写自变量的取值范围);
(2)求羽毛球落地点N离球网的水平距离(即NC的长);
(3)乙原地起跳后可接球的最大高度为2.4米,若乙因为接球高度不够而失球,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列条件求函数的表达式:
(1)已知变量x,y,t满足:y=t2﹣2,x=3﹣t.求y关于x的函数表达式;
(2)已知二次函数y=ax2+bx+c,当x=1时,y=2;当x=﹣2时,y=﹣7;当x=﹣1时,y=0.求这个二次函数的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com