
【题目】我们把函数y1=x2-3x+2(x>0)沿y轴翻折得到函数y2,函数y1与函数y2的图象合起来组成函数y3的图象.若直线y=kx+2与函数y3的图象刚好有两个交点,则满足条件的k的值为______.
【答案】-3<k<3
【解析】
根据翻折找出函数y2的解析式,将直线y=kx+2分别代入函数y1和y2的解析式中,求出x的值,根据x的取值范围列出关于k的一元一次不等式组,解不等式组即可得出结论.
解:依照题意画出图形,如图所示.
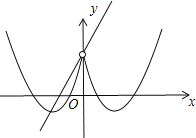
∵函数y1=x2-3x+2(x>0)沿y轴翻折得到函数y2,
∴y2=x2+3x+2(x<0).
若要直线y=kx+2与函数y3的图象刚好有两个交点,则需直线y=kx+2与y1、y2均有交点.
将直线y=kx+2分别代入y1、y2中得:
x2-(3+k)x=0,x2+(3-k)x=0.
解得:x1=3+k,x2=k-3,x3=0(舍去).
∵y1=x2-3x+2(x>0),
∴x1=3+k>0;
∵y2=x2+3x+2(x<0),
x2=k-3<0.
联立得:
![]() ,
,
解得:-3<k<3.
故答案为:-3<k<3.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 的位置如图所示:(每个小方格都是边长为1个单位长度的正方形)
的位置如图所示:(每个小方格都是边长为1个单位长度的正方形)
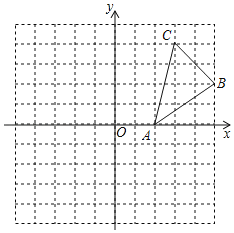
(1)画出![]() 关于点
关于点![]() 的中心对称图形△
的中心对称图形△![]() ;
;
(2)将![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() ,画出旋转后得到的△
,画出旋转后得到的△![]() ;
;
(3)请利用格点图,仅用无刻度的直尺画出![]() 边上的高
边上的高![]() (保留作图痕迹);
(保留作图痕迹);
(4)P为![]() 轴上一点,且△PBC是以BC为直角边的直角三角形.请直接写出点P的坐标.
轴上一点,且△PBC是以BC为直角边的直角三角形.请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一节数学课后,老师布置了一道课后练习题:
如图1,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,
上,![]() ,垂足为
,垂足为![]() ,
,![]() ,
,![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .求证:
.求证:![]() .
.
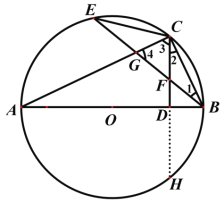
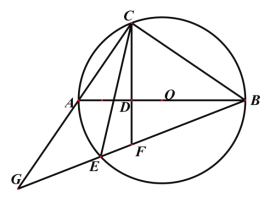
图1 图2
(1)本题证明的思路可用下列框图表示:
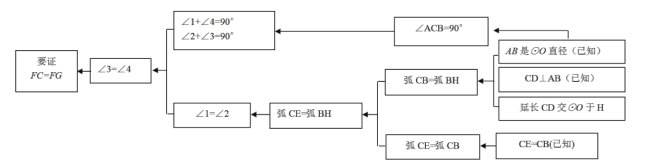
根据上述思路,请你完整地书写本题的证明过程.
(2)如图2,若点![]() 和点
和点![]() 在
在![]() 的两侧,
的两侧,![]() 、
、![]() 的延长线交于点
的延长线交于点![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,其余条件不变,(1)中的结论还成立吗?请说明理由;
,其余条件不变,(1)中的结论还成立吗?请说明理由;
(3)在(2)的条件下,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+3交x轴于点A(﹣1,0)和点B(3,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)连接BC,若点P为线段BC上的一个动点(不与点B、点C重合),过点P作直线PN⊥x轴于点N,交抛物线于点M,当△BCM面积最大时,求△BPN的周长.
(3)在(2)的条件下,当△BCM面积最大时,在抛物线的对称轴上是否存在点Q,使△CNQ为等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
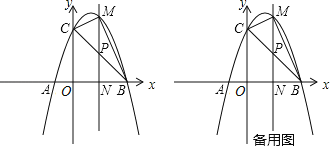
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE.
(1)求证:AD=DE;
(2)求∠DCE的度数;
(3)若BD=1,求AD,CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
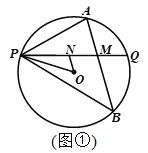
【题目】已知P是⊙O上一点,过点P作不过圆心的弦PQ,在劣弧PQ和优弧PQ上分别有动点A、B(不与P,Q重合),连接AP、BP. 若∠APQ=∠BPQ.
(1)如图1,当∠APQ=45°,AP=1,BP=2![]() 时,求⊙O的半径;
时,求⊙O的半径;
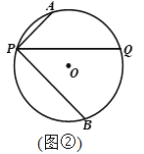
(2)如图2,选接AB,交PQ于点M,点N在线段PM上(不与P、M重合),连接ON、OP,若∠NOP+2∠OPN=90°,探究直线AB与ON的位置关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
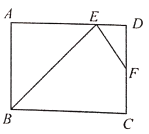
【题目】如图,矩形ABCD中,∠ABC的平分线交AD边于点E,点F是CD的中点,连接EF,若AB=8,且EF平分∠BED,则AD的长为_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为⊙O内接等边三角形,将△ABC绕圆心O旋转30°到△DEF处,连接AD、AE,则∠EAD的度数为( )
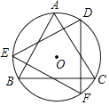
A.150°B.135°C.120°D.105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右图,正方形ABCD的边长为2,点E是BC边上一点,以AB为直径在正方形内作半圆
O,将△DCE沿DE翻折,点C刚好落在半圆O的点F处,则CE的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com