
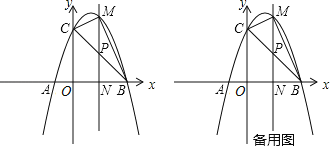
����Ŀ����ͼ��������y��ax2+bx+3��x���ڵ�A����1��0���͵�B��3��0������y�ύ�ڵ�C��
��1���������ߵĽ���ʽ��
��2������BC������PΪ�߶�BC�ϵ�һ�����㣨�����B����C�غϣ�������P��ֱ��PN��x���ڵ�N�����������ڵ�M������BCM������ʱ�����BPN���ܳ���
��3���ڣ�2���������£�����BCM������ʱ���������ߵĶԳ������Ƿ���ڵ�Q��ʹ��CNQΪ���������Σ������ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y����x2+2x+3 ��2��![]() ��3��������
��3��������
��������
��1����A��B��������뵽����ʽ����⼴�ɣ�
��2�����ֱ��BC�Ľ���ʽ��Ȼ�������BCM�ı���ʽ����һ�����κ����������ȡ���ֵ��������Ȼ�����ù��ɶ��������BPN���ܳ���
��3��C��N������֪���Q����Ϊ��1��a������������֮��ľ��빫ʽ��ʾ��CQ��QN��CNȻ��������������CQ��QN����CQ��CN����QN��CN������ʽ���.
�⣺��1������A����1��0����B��3��0������������ʽ�еã�![]() �����
�����![]() ��
��
�������߽���ʽΪy����x2+2x+3��
��2����ֱ��BC�Ľ���ʽΪ��y��kx+b��
���У�![]() ����ã�
����ã�![]() ��
��
��ֱ��BC�Ľ���ʽΪ��y����x+3��
��P��x����x+3������M��x����x2+2x+3����
��PM������x2+2x+3��������x+3������x2+3x��
��![]()
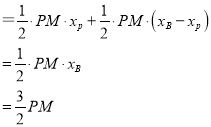 ��
��
��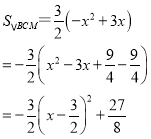
�൱![]() ʱ����BCM��������
ʱ����BCM��������
��ʱ![]() ��
��
��PN��ON��![]() ��
��
��![]() ��
��
��Rt��BPN�У��ɹ��ɶ����ã�![]() ��
��
![]() ��
��
�൱��BCM��������ʱ����BPN���ܳ�Ϊ![]() ��
��
��3���ɣ�2��֪P������Ϊ![]() ����
����![]() ��
��
��y����x2+2x+3������x��1��2+4��
�������ߵĶԳ���Ϊx��1��
��Q��1��a������C��0��3����![]() ��
��
��![]() ��
��![]() ������֮����빫ʽ����
������֮����빫ʽ����
����CNQΪ���������Σ��ɷ����������
�ٵ�CQ��QNʱ��![]() ����ã�
����ã�![]() ��
��
���Q������Ϊ![]() ��
��
�ڵ�CQ��CNʱ��![]() ����ã�
����ã�![]() ��
��
���Q������Ϊ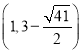 ��
��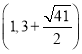 ��
��
�۵�QN��CNʱ��![]() ����ã�
����ã�![]() ��
��
���Q������Ϊ![]() ��
��![]() ��
��
�ۺ����Ͽɵõ�Q������Ϊ![]() ��
��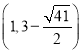 ��
��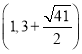 ��
��![]() ��
��![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=4��AD=2��EΪAB���е㣬FΪEC��һ���㣬PΪDF�е㣬����PB����PB����Сֵ��_____.
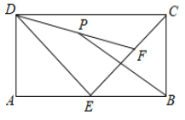
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
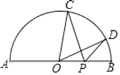
����Ŀ����ͼ���ڰ�Բ��O�У�ֱ��AB=4����C��D�ǰ�Բ�����㣬����BOC=84������BOD=36����PΪֱ����һ�㣬��PC+PD����СֵΪ�� ��
A.4B.2![]() C.2
C.2![]() D.2
D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
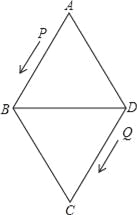
����Ŀ����ͼ������ABCD�ı߳�Ϊ24���ף���A=60������P�ӵ�A��������·AB��BD�������˶�����Q�ӵ�Dͬʱ��������·DC��CB��BA�������˶���
��1����BD�ij���
��2����֪��P��Q�˶����ٶȷֱ�Ϊ4����/�룬5����/�룬����12���P��Q�ֱ�M��N���㣬�����ǵĴ�С���з��࣬����ȷ����AMN����һ�������Σ���˵�����ɣ�
��3���裨2���еĵ�P��Q�ֱ��M��Nͬʱ��ԭ·���أ���P���ٶȲ��䣬��Q���ٶȸı�Ϊa����/�룬����3���P��Q�ֱ�E��F���㣬����BEF�루2���е���AMN���ƣ�����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
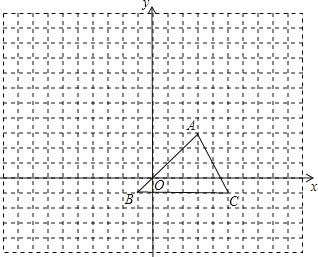
����Ŀ����ͼ��ʾ������������ABC�Ķ����������ϣ��ڽ���ƽ��ֱ������ϵ��B��������(-1��-1)
(1)�ѡ�ABC����ƽ��10��õ�![]() ������
������![]() ��
��
(2)����![]() ����x��ԳƵ�ͼ��
����x��ԳƵ�ͼ��![]() ��
��
(3)�ѡ�ABC�Ƶ�C˳ʱ����ת90����õ�![]() ������
������![]() �������
�������![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����в�������һ�˻����������У���ÿ�ִ�Ⱦ��һ�˽�ƽ������x�ˣ�
��1����һ�ֺ�������Ϊ �����ú�x�Ĵ���ʽ��ʾ��
��2���ڽ���ڶ��ִ�Ⱦ֮ǰ������λ���߱���ʱ���벢�������ʵڶ��ִ�Ⱦ���ܹ��Ƿ����21�˻����������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ǰѺ���y1��x2��3x��2(x��0)��y�ᷭ�۵õ�����y2������y1�뺯��y2��ͼ���������ɺ���y3��ͼ��.��ֱ��y��kx��2�뺯��y3��ͼ��պ����������㣬������������k��ֵΪ______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD�ı߳�Ϊ4��һ���Ե�AΪ�����45����Ƶ�A��ת���ǵ����߷ֱ���BC��DC���ӳ��߽��ڵ�E��F������EF����CE=a��CF=b��
��1����ͼ1����a=4![]() ʱ����b��ֵ��
ʱ����b��ֵ��
��2����a=4ʱ����ͼ2�����b��ֵ��
��3����ͼ3����д����EAF�Ƶ�A��ת�Ĺ�����a��b����Ĺ�ϵʽ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
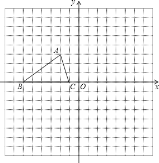
����Ŀ����ͼ����֪��ABC���������������ֱ�ΪA����2��3����B����6��0����C����1��0����
��1��������ABC����ԭ������ĶԳƵ������Ρ�A��B��C�䣻
��2������ABC������ԭ��O��ʱ����ת90�㣬����ͼ�Σ�ֱ��д����B�Ķ�Ӧ��B������ꣻ
��3����ֱ��д������A��B��CΪ�����ƽ���ı��εĵ��ĸ�����D�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com