
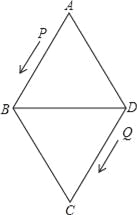
°æƒø°ø»ÁÕº£¨¡‚–ŒABCDµƒ±þ≥§Œ™24¿Â√◊£¨°œA=60°„£¨µ„P¥”µ„A≥ˆ∑¢—ÿœþ¬∑AB°˙BD◊˜‘»ÀŸ‘À∂Ø£¨µ„Q¥”µ„DÕ¨ ±≥ˆ∑¢—ÿœþ¬∑DC°˙CB°˙BA◊˜‘»ÀŸ‘À∂Ø£Æ
£®1£©«ÛBDµƒ≥§£ª
£®2£©“—÷™µ„P°¢Q‘À∂صƒÀŸ∂»∑÷±Œ™4¿Â√◊/√Σ¨5¿Â√◊/√Σ¨æ≠π˝12√Î∫Û£¨P°¢Q∑÷±µΩ¥ÔM°¢N¡Ωµ„£¨»Ù∞¥Ω«µƒ¥Û–°Ω¯––∑÷¿ý£¨«Îƒ„»∑∂®°˜AMN «ƒƒ“ª¿ý»˝Ω«–Œ£¨≤¢Àµ√˜¿Ì”…£ª
£®3£©…Ë£®2£©÷–µƒµ„P°¢Q∑÷±¥”M°¢NÕ¨ ±—ÿ‘≠¬∑∑µªÿ£¨µ„PµƒÀŸ∂»≤ª±‰£¨µ„QµƒÀŸ∂»∏ƒ±‰Œ™a¿Â√◊/√Σ¨æ≠π˝3√Î∫Û£¨P°¢Q∑÷±µΩ¥ÔE°¢F¡Ωµ„£¨»Ù°˜BEF”Σ®2£©÷–µƒ°˜AMNœýÀ∆£¨ ‘«Ûaµƒ÷µ£Æ
°æ¥∞∏°ø£®1£©BD=24£®2£©°˜AMN «÷±Ω«»˝Ω«–Œ£®3£©2ªÚ6ªÚ12
°æΩ‚Œˆ°ø
‘£®1£©∏˘æð¡‚–Œµƒ–‘÷ ÷§°˜ABD «µ»±þ»˝Ω«–Œº¥ø…£ª
£®2£©«Û≥ˆP Q◊þµƒæý¿Î£¨‘Ÿ∏˘æðµ»—¸»˝Ω«–Œ–‘÷ º¥ø…Õ∆≥ˆ¥∞∏£ª
£®3£©∑÷Œ™»˝÷÷«Èøˆ£∫∏˘æðœýÀ∆£¨µ√µΩ±»¿˝ Ω£¨«Û≥ˆQ◊þµƒæý¿Î£¨º¥ø…«Û≥ˆ¥∞∏£Æ
‘Ã‚Ω‚Œˆ£∫£®1£©°þ¡‚–ŒABCD£¨
°ýAB=AD£¨
°þ°œA=60°„£¨
°ý°˜ABD «µ»±þ»˝Ω«–Œ£¨
°ýBD=AB=24¿Â√◊£Æ
¥£∫BD=24¿Â√◊£Æ
£®2£©12√Î ±£¨P◊þ¡À4°¡12=48£¨
°þAB+BD=24+24=48£¨
°ýPµΩDµ„£¨
Õ¨¿ÌQµΩABµƒ÷–µ„…œ£¨
°þAD=BD£¨
°ýMN°ÕAB£¨
°ý°˜AMN «÷±Ω«»˝Ω«–Œ£Æ
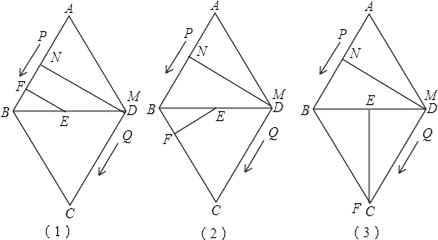
£®3£©”–»˝÷÷«Èøˆ£∫»ÁÕº£®2£©
°œANM=°œEFB=90°„£¨°œA=°œDBF=60°„£¨DE=3°¡4=12=![]() AD£¨
AD£¨
∏˘æðœýÀ∆»˝Ω«–Œ–‘÷ µ√£∫BF=![]() AN=6£¨
AN=6£¨
°ýNB+BF=12+6=18£¨
°ýa=18°¬3=6£¨
Õ¨¿Ì£∫»ÁÕº£®1£©«Û≥ˆa=2£ª
»ÁÕº£®3£©a=12£Æ
°ýaµƒ÷µ «2ªÚ6ªÚ12£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº1£¨‘⁄æÿ–Œ![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨Ω´
£¨Ω´![]() »∆µ„
»∆µ„![]() ¥”
¥”![]() ¥¶ø™ º∞¥À≥ ±’Î∑ΩœÚ–˝◊™£¨
¥¶ø™ º∞¥À≥ ±’Î∑ΩœÚ–˝◊™£¨![]() Ωª±þ
Ωª±þ![]() £®ªÚ
£®ªÚ![]() £©”⁄µ„
£©”⁄µ„![]() £¨
£¨![]() Ωª±þ
Ωª±þ![]() £®ªÚ
£®ªÚ![]() £©”⁄µ„
£©”⁄µ„![]() £¨µ±
£¨µ±![]() –˝◊™÷¡
–˝◊™÷¡![]() ¥¶ ±£¨
¥¶ ±£¨![]() Õ£÷π–˝◊™.
Õ£÷π–˝◊™.
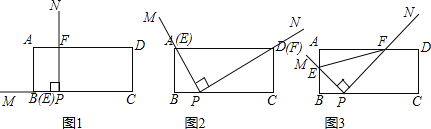
£®1£©Ãÿ ‚«È–Œ£∫»ÁÕº2£¨∑¢œ÷µ±![]() π˝µ„
π˝µ„![]() ±£¨PN“≤«°«…π˝µ„
±£¨PN“≤«°«…π˝µ„![]() £¨¥À ±
£¨¥À ±![]()
![]() £®ÃÓ°∞°’°±ªÚ°∞°◊°±£©£ª
£®ÃÓ°∞°’°±ªÚ°∞°◊°±£©£ª
£®2£©¿ý±»ÃΩæø£∫»ÁÕº3£¨‘⁄–˝◊™π˝≥Ã÷–£¨![]() µƒ÷µ «∑ÒŒ™∂®÷µ£ø»Ù «£¨«Î«Û≥ˆ∏√∂®÷µ£ª»Ù≤ª «£¨«ÎÀµ√˜¿Ì”….
µƒ÷µ «∑ÒŒ™∂®÷µ£ø»Ù «£¨«Î«Û≥ˆ∏√∂®÷µ£ª»Ù≤ª «£¨«ÎÀµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥◊®¬ÙµÍ◊º±∏π∫Ω¯º◊°¢““¡Ω÷÷‘À∂Ø–¨£¨∆‰Ω¯º€∫Õ €º€»Áœ¬±ÌÀ˘ æ°£“—÷™”√3000‘™π∫Ω¯º◊÷÷‘À∂Ø–¨µƒ ˝¡ø”Δ√2400‘™π∫Ω¯““÷÷‘À∂Ø–¨µƒ ˝¡øœýÕ¨.
‘À∂Ø–¨º€∏Ò | º◊ | ““ |
Ω¯º€‘™/À´) | m | m-30 |
€º€(‘™/À´) | 300 | 200 |
(1)«Ûmµƒ÷µ£ª
(2)“™ ππ∫Ω¯µƒº◊£¨““¡Ω÷÷‘À∂Ø–¨π≤200À´µƒ◊п˚»Û≤ª…Ÿ”⁄21700‘™«“≤ª≥¨π˝22300‘™£¨Œ ∏√◊®¬ÙµÍ”–º∏÷÷Ω¯ªı∑Ω∞∏?
(3)‘⁄(2)µƒÃıº˛œ¬£¨◊®¬ÙµÍæˆ∂®∂‘º◊÷÷‘À∂Ø–¨√øÀ´”≈ªða(60<a<80)‘™≥ˆ €£¨““÷÷‘À∂Ø–¨º€∏Ò≤ª±‰£¨ƒ«√¥∏√◊®¬ÙµÍ“™ªÒµ√◊Ó¥Û¿˚»Û”¶»Á∫ŒΩ¯ªı?
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
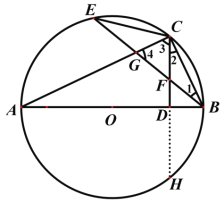
°æƒø°ø»ÁÕº£¨BE «°—Oµƒ÷±æ∂£¨µ„A‘⁄EBµƒ—”≥§œþ…œ£¨œ“PD°ÕBE£¨¥π◊„Œ™C£¨¡¨Ω”OD£¨
°œAOD=°œAPC£Æ

£®1£©«Û÷§£∫AP «°—Oµƒ«–œþ£ª
£®2£©»Ù°—Oµƒ∞Îæ∂ «4£¨AP=4![]() £¨«ÛÕº÷–“ı”∞≤ø∑÷µƒ√ʪ˝£Æ
£¨«ÛÕº÷–“ı”∞≤ø∑÷µƒ√ʪ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“ªΩ⁄ ˝—ßøŒ∫Û£¨¿œ ¶≤º÷√¡À“ªµ¿øŒ∫Û¡∑œ∞£∫
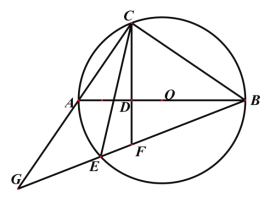
»ÁÕº1£¨![]() «
«![]() µƒ÷±æ∂£¨µ„
µƒ÷±æ∂£¨µ„![]() ‘⁄
‘⁄![]() …œ£¨
…œ£¨![]() £¨¥π◊„Œ™
£¨¥π◊„Œ™![]() £¨
£¨![]() £¨
£¨![]() ∑÷±Ωª
∑÷±Ωª![]() °¢
°¢![]() ”⁄µ„
”⁄µ„![]() °¢
°¢![]() .«Û÷§£∫
.«Û÷§£∫![]() .
.
Õº1 Õº2
£®1£©±æÂ÷§√˜µƒÀº¬∑ø…”√œ¬¡–øÚÕº±Ì æ£∫
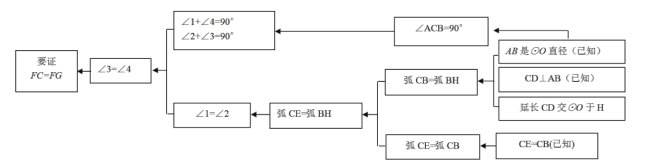
∏˘æð…œ ˆÀº¬∑£¨«Îƒ„ÕÍ’˚µÿ È–¥±æµƒ÷§√˜π˝≥Ã.
£®2£©»ÁÕº2£¨»Ùµ„![]() ∫Õµ„
∫Õµ„![]() ‘⁄
‘⁄![]() µƒ¡Ω≤ý£¨
µƒ¡Ω≤ý£¨![]() °¢
°¢![]() µƒ—”≥§œþΩª”⁄µ„
µƒ—”≥§œþΩª”⁄µ„![]() £¨
£¨![]() µƒ—”≥§œþΩª
µƒ—”≥§œþΩª![]() ”⁄µ„
”⁄µ„![]() £¨∆‰”ýÃıº˛≤ª±‰£¨£®1£©÷–µƒΩ·¬€ªπ≥…¡¢¬£ø«ÎÀµ√˜¿Ì”…£ª
£¨∆‰”ýÃıº˛≤ª±‰£¨£®1£©÷–µƒΩ·¬€ªπ≥…¡¢¬£ø«ÎÀµ√˜¿Ì”…£ª
£®3£©‘⁄£®2£©µƒÃıº˛œ¬£¨»Ù![]() £¨
£¨![]() £¨«Û
£¨«Û![]() µƒ≥§.
µƒ≥§.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº,µ„O «µ»±þ![]() ƒ⁄“ªµ„
ƒ⁄“ªµ„![]() Ω´
Ω´![]() »∆µ„C∞¥À≥ ±’Î∑ΩœÚ–˝◊™
»∆µ„C∞¥À≥ ±’Î∑ΩœÚ–˝◊™![]() µ√
µ√![]() ,¡¨Ω”
,¡¨Ω”![]() “—÷™
“—÷™![]()
![]() £Æ
£Æ
![]() «Û÷§£∫
«Û÷§£∫![]() «µ»±þ»˝Ω«–Œ£ª
«µ»±þ»˝Ω«–Œ£ª
![]() µ±
µ±![]() ±, ‘≈–∂œ
±, ‘≈–∂œ![]() µƒ–Œ◊¥,≤¢Àµ√˜¿Ì”…£ª
µƒ–Œ◊¥,≤¢Àµ√˜¿Ì”…£ª
![]() ÃΩæø£∫µ±
ÃΩæø£∫µ±![]() Œ™∂ý…Ÿ∂» ±,
Œ™∂ý…Ÿ∂» ±,![]() «µ»—¸»˝Ω«–Œ£Æ
«µ»—¸»˝Ω«–Œ£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþy£Ωax2+bx+3Ωªx÷·”⁄µ„A£®©Å1£¨0£©∫Õµ„B£®3£¨0£©£¨”Îy÷·Ωª”⁄µ„C£Æ
£®1£©«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
£®2£©¡¨Ω”BC£¨»Ùµ„PŒ™œþ∂ŒBC…œµƒ“ª∏ˆ∂ص„£®≤ª”ε„B°¢µ„C÷ÿ∫œ£©£¨π˝µ„P◊˜÷±œþPN°Õx÷·”⁄µ„N£¨Ωª≈◊ŒÔœþ”⁄µ„M£¨µ±°˜BCM√ʪ˝◊Ó¥Û ±£¨«Û°˜BPNµƒ÷Ð≥§£Æ
£®3£©‘⁄£®2£©µƒÃıº˛œ¬£¨µ±°˜BCM√ʪ˝◊Ó¥Û ±£¨‘⁄≈◊ŒÔœþµƒ∂‘≥∆÷·…œ «∑ҥʑ⁄µ„Q£¨ π°˜CNQŒ™µ»—¸»˝Ω«–Œ£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆµ„Qµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
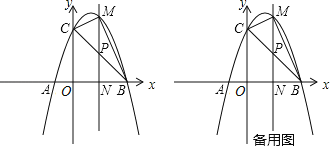
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
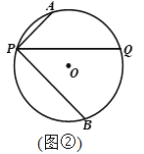
°æƒø°ø“—÷™P «°—O…œ“ªµ„£¨π˝µ„P◊˜≤ªπ˝‘≤–ƒµƒœ“PQ£¨‘⁄¡”ª°PQ∫Õ”≈ª°PQ…œ∑÷±”–∂ص„A°¢B(≤ª”ÎP£¨Q÷ÿ∫œ)£¨¡¨Ω”AP°¢BP. »Ù°œAPQ=°œBPQ.
(1)»ÁÕº1£¨µ±°œAPQ=45°„£¨AP=1£¨BP=2![]() ±£¨«Û°—Oµƒ∞Îæ∂£ª
±£¨«Û°—Oµƒ∞Îæ∂£ª
(2)»ÁÕº2£¨—°Ω”AB£¨ΩªPQ”⁄µ„M£¨µ„N‘⁄œþ∂ŒPM…œ(≤ª”ÎP°¢M÷ÿ∫œ)£¨¡¨Ω”ON°¢OP£¨»Ù°œNOP+2°œOPN=90°„£¨ÃΩæø÷±œþAB”ÎONµƒŒª÷√πÿœµ£¨≤¢÷§√˜.
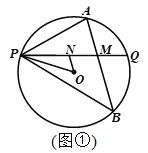
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
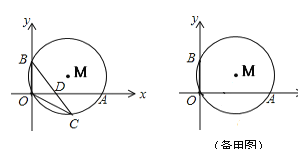
°æƒø°ø»ÁÕº£¨°—Mæ≠π˝Oµ„£¨≤¢«“”Îx÷·°¢y÷·∑÷±Ωª”⁄A°¢B¡Ωµ„£¨œþ∂ŒOA°¢OB£®OA£æOB£©µƒ≥§ «∑Ω≥Ã![]() µƒ¡Ω∏˘£Æ
µƒ¡Ω∏˘£Æ
£®1£©«Ûœþ∂ŒOA°¢OBµƒ≥§£ª
£®2£©»Ùµ„C‘⁄¡”ª°OA…œ,¡¨Ω·BCΩªOA”⁄D£¨µ±OC2£ΩCD°§CB ±£¨«Ûµ„Cµƒ◊¯±Í£ª
£®3£©»Ùµ„C‘⁄”≈ª°OA…œ£¨◊˜÷±œþBCΩªx÷·”⁄D£¨ «∑ҥʑ⁄°˜COB∫Õ°˜CDOœýÀ∆£¨»Ù¥Ê‘⁄£¨«Û≥ˆµ„Cµƒ◊¯±Í£¨»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com