
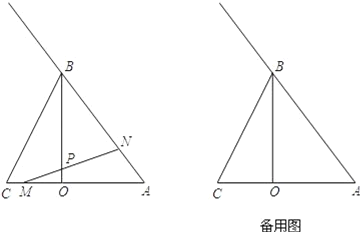
【题目】如图,⊙M经过O点,并且与x轴、y轴分别交于A、B两点,线段OA、OB(OA>OB)的长是方程![]() 的两根.
的两根.
(1)求线段OA、OB的长;
(2)若点C在劣弧OA上,连结BC交OA于D,当OC2=CD·CB时,求点C的坐标;
(3)若点C在优弧OA上,作直线BC交x轴于D,是否存在△COB和△CDO相似,若存在,求出点C的坐标,若不存在,请说明理由.
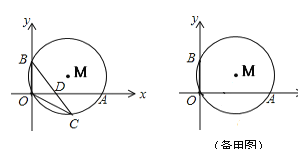
【答案】(1)OA=12,OB=5;(2)C点坐标为(6,-4);(3)存在. C点坐标为(6,9).
【解析】
(1)利用因式分解法解方程即可得到OA=12,OB=5;
(2)连接AB、AC、MC,MC与OA交于F,如图1,由OC2=CDCB,∠OCD=∠BCO,根据相似三角形的判定方法即可得到△COD∽△CBO,则∠2=∠1,而根据圆周角定理有∠1=∠3,所以∠2=∠3,得到弧AC=弧OC,根据垂径定理得MC⊥OA,OF=AF=![]() OA=6,然后根据圆周角定理由∠AOB=90°得AB为⊙M的直径,则在Rt△AOB中,根据勾股定理可计算出AB=13,得到MC=
OA=6,然后根据圆周角定理由∠AOB=90°得AB为⊙M的直径,则在Rt△AOB中,根据勾股定理可计算出AB=13,得到MC=![]() ,易得MF=
,易得MF=![]() OB=
OB=![]() ,则FC=MC-MF=4,于是得到C点坐标为(6,-4);
,则FC=MC-MF=4,于是得到C点坐标为(6,-4);
(3)连接AC,连接CM并延长交OA于F,如图2,若CA=CO,则∠COA=∠CAO,根据邻补角的定义得∠COA+∠COD=180°,根据圆内接四边形的性质得∠CAO+∠CBO=180°,则∠COD=∠CBO,加上∠OCD=∠DCO,根据相似的判定方法即可得到△CBO∽△COD;由CA=CO得弧CA=弧CO,根据垂径定理得CF⊥AC,由(2)得MF=![]() ,CM=
,CM=![]() ,OF=6,则CF=CM+MF=9,于是得到C点坐标为(6,9).
,OF=6,则CF=CM+MF=9,于是得到C点坐标为(6,9).
(1)∵(x-12)(x-5)=0,
∴x1=12,x2=5,
∴OA=12,OB=5;
(2)连接AB、AC、MC,MC与OA交于F,如图1,
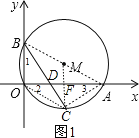
∵OC2=CDCB,即OC:CD=CB:OC,
而∠OCD=∠BCO,
∴△COD∽△CBO,
∴∠2=∠1,
∵∠1=∠3,
∴∠2=∠3,
∴弧AC=弧OC,
∴MC⊥OA,
∴OF=AF=![]() OA=6,
OA=6,
∵∠AOB=90°,
∴AB为⊙M的直径,
在Rt△AOB中,OA=12,OB=5,
∴AB=13,
∴MC=![]() ,
,
∵MF为△AOB的中位线,
∴MF=![]() OB=
OB=![]() ,
,
∴FC=MC-MF=4,
∴C点坐标为(6,-4);
(3)存在.
连接AC,连接CM并长交OA于F,如图2,
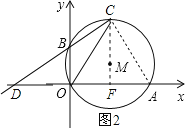
若CA=CO,则∠COA=∠CAO,
∵∠COA+∠COD=180°,∠CAO+∠CBO=180°,
∴∠COD=∠CBD,而∠OCD=∠DOC,
∴△CBO∽△COD,
∵CA=CO,
∴弧CA=弧CO,
∴CF⊥AC,
由(2)得MF=![]() ,CM=
,CM=![]() ,OF=6,
,OF=6,
∴CF=CM+MF=9,
∴C点坐标为(6,9).


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
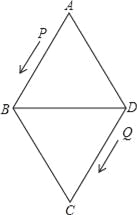
【题目】如图,菱形ABCD的边长为24厘米,∠A=60°,点P从点A出发沿线路AB→BD作匀速运动,点Q从点D同时出发沿线路DC→CB→BA作匀速运动.
(1)求BD的长;
(2)已知点P、Q运动的速度分别为4厘米/秒,5厘米/秒,经过12秒后,P、Q分别到达M、N两点,若按角的大小进行分类,请你确定△AMN是哪一类三角形,并说明理由;
(3)设(2)中的点P、Q分别从M、N同时沿原路返回,点P的速度不变,点Q的速度改变为a厘米/秒,经过3秒后,P、Q分别到达E、F两点,若△BEF与(2)中的△AMN相似,试求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的边长为4,一个以点A为顶点的45°角绕点A旋转,角的两边分别与BC、DC的延长线交于点E、F,连接EF,设CE=a,CF=b.
(1)如图1,当a=4![]() 时,求b的值;
时,求b的值;
(2)当a=4时,如图2,求出b的值;
(3)如图3,请写出∠EAF绕点A旋转的过程中a、b满足的关系式,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
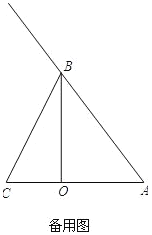
【题目】如图,已知BO是△ABC的AC边上的高,其中BO=8,AO=6,CO=4,点M以2个单位长度/秒的速度自C向A在线段CA上作匀速运动,同时点N以5个单位长度/秒的速度自A向B在射线AB上作匀速运动,MN交OB于点P.当M运动到点A时,点M、N同时停止运动.设点M运动时间为t.
(1)线段AN的取值范围是______.
(2)当0<t<2时,
①求证:MN:NP为定值.
②若△BNP与△MNA相似,求CM的长.
(3)当2<t<5时,若△BNP是等腰三角形,求CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】沙坪坝区各街道居民积极响应“创文明城区”活动,据了解,某街道居民人口共有7.5万人,街道划分为A,B两个社区,B社区居民人口数量不超过A社区居民人口数量的2倍.
(1)求A社区居民人口至少有多少万人?
(2)街道工作人员调查A,B两个社区居民对“社会主义核心价值观”知晓情况发现:A社区有1.2万人知晓,B社区有1.5万人知晓,为了提高知晓率,街道工作人员用了两个月的时间加强宣传,A社区的知晓人数平均月增长率为m%,B社区的知晓人数第一个月增长了![]() m%,第二月在第一个月的基础上又增长了2m%,两个月后,街道居民的知晓率达到92%,求m的值.
m%,第二月在第一个月的基础上又增长了2m%,两个月后,街道居民的知晓率达到92%,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
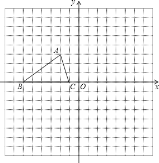
【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
(1)画出△ABC关于原点成中心对称的三角形△A′B′C′;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点B″的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一元二次方程![]() 满足
满足![]() ,那么我们称这个方程为“凤凰”方程.已知
,那么我们称这个方程为“凤凰”方程.已知![]() 是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是 ( )
是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E,F分别在边AB,BC上,AF=DE,AF和DE相交于点G.
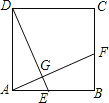
(1)观察图形,写出图中所有与∠AED相等的角.
(2)选择图中与∠AED相等的任意一个角,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com