
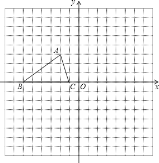
【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
(1)画出△ABC关于原点成中心对称的三角形△A′B′C′;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点B″的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
【答案】(1)图略;(2)图略,点B″的坐标为(0,﹣6);(3)点D坐标为(﹣7,3)或(3,3)或(﹣5,﹣3).
【解析】
(1)根据网格结构找出点A、B、C关于原点对称的点A′、B′、C′的位置,然后顺次连接即可;
(2)根据网格结构找出点A、B、C绕坐标原点O逆时针旋转90°的对应点的位置,然后顺次连接即可,再根据平面直角坐标系写出点B的对应点的坐标;
(3)分AB、BC、AC是平行四边形的对角线三种情况解答.
解:(1)如图所示△A′B′C′即为所求;
(2)如图所示,△![]() 即为所求;
即为所求;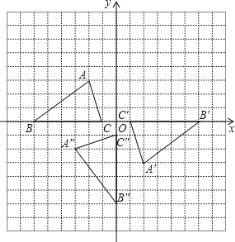
(3)D(-7,3)或(-5,-3)或(3,3).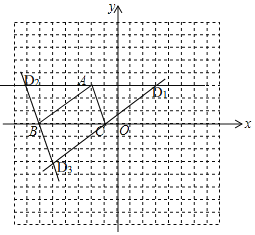
当以BC为对角线时,点D3的坐标为(-5,-3);
当以AB为对角线时,点D2的坐标为(-7,3);
当以AC为对角线时,点D1坐标为(3,3).


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:初中数学 来源: 题型:
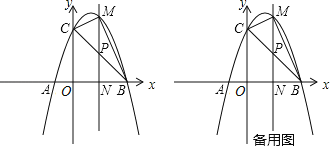
【题目】如图,抛物线y=ax2+bx+3交x轴于点A(﹣1,0)和点B(3,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)连接BC,若点P为线段BC上的一个动点(不与点B、点C重合),过点P作直线PN⊥x轴于点N,交抛物线于点M,当△BCM面积最大时,求△BPN的周长.
(3)在(2)的条件下,当△BCM面积最大时,在抛物线的对称轴上是否存在点Q,使△CNQ为等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为⊙O内接等边三角形,将△ABC绕圆心O旋转30°到△DEF处,连接AD、AE,则∠EAD的度数为( )
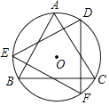
A.150°B.135°C.120°D.105°
查看答案和解析>>
科目:初中数学 来源: 题型:
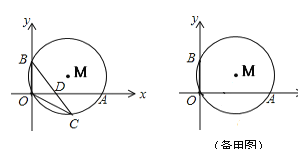
【题目】如图,⊙M经过O点,并且与x轴、y轴分别交于A、B两点,线段OA、OB(OA>OB)的长是方程![]() 的两根.
的两根.
(1)求线段OA、OB的长;
(2)若点C在劣弧OA上,连结BC交OA于D,当OC2=CD·CB时,求点C的坐标;
(3)若点C在优弧OA上,作直线BC交x轴于D,是否存在△COB和△CDO相似,若存在,求出点C的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
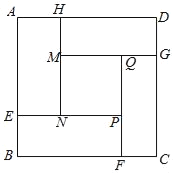
【题目】创客联盟的队员想用3D打印完成一幅边长为6米的正方形作品ABCD,设计图案如图所示(四周阴影是四个全等的矩形,用材料甲打印;中心区是正方形MNPQ,用材料乙打印).在打印厚度保持相同的情况下,两种材料的消耗成本如下表:
材料 | 甲 | 乙 |
价格(元/米2) | 80 | 50 |
设矩形的较短边AH的长为x米,打印材料的总费用为y元.
(1)MQ的长为 米(用含x的代数式表示);
(2)求y关于x的函数解析式;
(3)当中心区的边长不小于2米时,预备材料的购买资金2800元够用吗?请利用函数的增减性来说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.
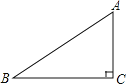
(1)以直线BC为轴,把△ABC旋转一周,求所得圆锥的底面圆周长.
(2)以直线AC为轴,把△ABC旋转一周,求所得圆锥的侧面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右图,正方形ABCD的边长为2,点E是BC边上一点,以AB为直径在正方形内作半圆
O,将△DCE沿DE翻折,点C刚好落在半圆O的点F处,则CE的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠ABC=90°,将△ABC绕点B逆时针旋转90°后,点A的对应点为点D,点C的对应点为点E,直线DE与直线AC交于点F,连接FB.
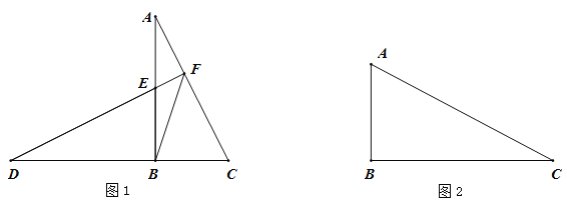
(1)如图1,当∠BAC<45°时,
①求证:DF⊥AC;
②求∠DFB的度数;
(2)如图2,当∠BAC>45°时,
①请依题意补全图2;
②用等式表示线段FC,FB,FE之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
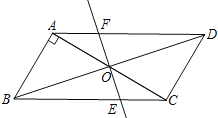
【题目】已知,如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=![]() ,对角线AC,BD交于O点,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
,对角线AC,BD交于O点,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
(1)求证:当旋转角为90°时,四边形ABEF是平行四边形;
(2)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如能,说明理由并求出此时AC绕点O顺时针旋转的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com