
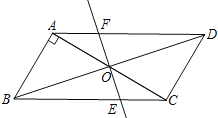
【题目】已知,如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=![]() ,对角线AC,BD交于O点,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
,对角线AC,BD交于O点,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
(1)求证:当旋转角为90°时,四边形ABEF是平行四边形;
(2)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如能,说明理由并求出此时AC绕点O顺时针旋转的度数.
【答案】(1)见解析 (2)见解析
【解析】
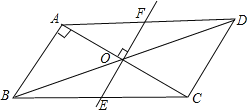
(1)根据∠BAC=∠AOF=90°推出AB∥EF,根据平行四边形性质得出AF∥BE,即可推出四边形ABEF是平行四边形;
(2)证△DFO≌△BEO,推出OF=OE,得出四边形BEDF是平行四边形,根据勾股定理求出AC,求出OA=AB=1,求出∠AOB=45°,根据∠AOF=45°,推出EF⊥BD,根据菱形的判定推出即可.
(1)证明:∵∠AOF=90°,∠BAO=90°,
∴AB∥EF,
又∵平行四边形ABCD,
∴AF∥EB,
∴四边形ABEF是平行四边形;
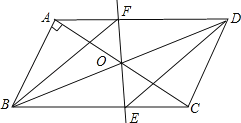
(2)当旋转角∠AOF=45°时,四边形BEDF是菱形,理由如下:
∵平行四边形ABCD,
∴AD∥BC,BO=DO,
∴∠FDO=∠EBO,∠DFO=∠BEO,
在△DFO和△BEO中
∵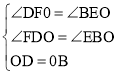 ,
,
∴△DFO≌△BEO(AAS),
∴OF=OE,
∴四边形BEDF是平行四边形,
∵AB=1,BC=![]() ,
,
∴在Rt△BAC中,由勾股定理得:AC=2,
∴AO=1=AB,
∴∠AOB=45°,
又∵∠AOF=45°,
∴∠BOF=90°,
∴BD⊥EF,
∴四边形BEDF是菱形,
即在旋转过程中,四边形BEDF能是菱形,此时AC绕点O顺时针旋转的度数是45°.


科目:初中数学 来源: 题型:
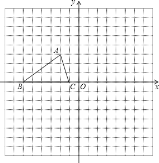
【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
(1)画出△ABC关于原点成中心对称的三角形△A′B′C′;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点B″的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列是关于四个图案的描述.
图1所示是太极图,俗称“阴阳鱼”,该图案关于外圈大圆的圆心中心对称;
图2所示是一个正三角形内接于圆;
图3所示是一个正方形内接于圆;
图4所示是两个同心圆,其中小圆的半径是外圈大圆半径的三分之二.
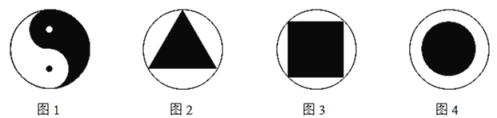
这四个图案中,阴影部分的面积不小于该图案外圈大圆面积一半的是( )
A.图1和图3B.图2和图3C.图2和图4D.图1和图4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E,F分别在边AB,BC上,AF=DE,AF和DE相交于点G.
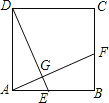
(1)观察图形,写出图中所有与∠AED相等的角.
(2)选择图中与∠AED相等的任意一个角,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小芳家的落地窗(线段DE)与公路(直线PQ)互相平行,她每天做完作业后都会在点A处向窗外的公路望去.
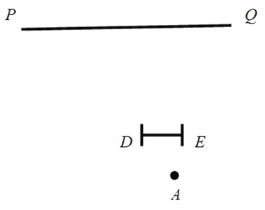
(1)请在图中画出小芳能看到的那段公路并记为BC.
(2)小芳很想知道点A与公路之间的距离,于是她想到了一个办法.她测出了邻家小彬在公路BC段上走过的时间为10秒,又测量了点A到窗的距离是4米,且窗DE的长为3米,若小彬步行的平均速度为1.2米/秒,请你帮助小芳计算出点A到公路的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=25°,O为AB的中点. 将OA绕点O逆时针旋转θ °至OP(0<θ<180),当△BCP恰为轴对称图形时,θ的值为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
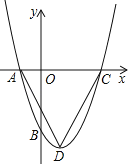
【题目】如图,抛物线y=x2+bx+c与x轴交于A,C两点,与y轴交于B点,抛物线的顶点为点D,已知点A的坐标为(﹣1,0),点B的坐标为(0,﹣3).
(1)求抛物线的解析式及顶点D的坐标.
(2)求△ACD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
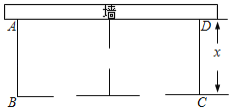
【题目】某农场要建一个饲养场(长方形![]() ,饲养场的一面靠墙(墙最大可用长度为27米),另三边用木栏围成,中间也用木栏隔开,分成两个场地,并在如图所示的三处各留1米宽的门(不用木栏),建成后木栏总长60米,设饲养场(长方形
,饲养场的一面靠墙(墙最大可用长度为27米),另三边用木栏围成,中间也用木栏隔开,分成两个场地,并在如图所示的三处各留1米宽的门(不用木栏),建成后木栏总长60米,设饲养场(长方形![]() 的宽为
的宽为![]() 米.
米.
(1)求饲养场的长![]() (用含
(用含![]() 的代数式表示).
的代数式表示).
(2)若饲养场的面积为![]() ,求
,求![]() 的值.
的值.
(3)当![]() 为何值时,饲养场的面积最大,此时饲养场达到的最大面积为多少
为何值时,饲养场的面积最大,此时饲养场达到的最大面积为多少![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中(BC>AB),过A作AF⊥BC,垂足为F,过C作CH⊥AB,垂足为H,交AF于G,点E为FC上一点,且GE⊥ED.
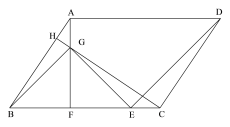
(1)若FC=2BF=4,AB=![]() ,求平行四边形ABCD的面积.
,求平行四边形ABCD的面积.
(2) 若AF=FC,F为BE中点,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com