
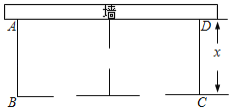
����Ŀ��ijũ��Ҫ��һ����������������![]() ����������һ�濿ǽ��ǽ�����ó���Ϊ27�ף�����������ľ��Χ�ɣ��м�Ҳ��ľ���������ֳ��������أ�������ͼ��ʾ����������1�����ţ�����ľ���������ɺ�ľ���ܳ�60�ף�����������������
����������һ�濿ǽ��ǽ�����ó���Ϊ27�ף�����������ľ��Χ�ɣ��м�Ҳ��ľ���������ֳ��������أ�������ͼ��ʾ����������1�����ţ�����ľ���������ɺ�ľ���ܳ�60�ף�����������������![]() �Ŀ�Ϊ
�Ŀ�Ϊ![]() �ף�
�ף�
��1�����������ij�![]() ���ú�
���ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2���������������Ϊ![]() ����
����![]() ��ֵ��
��ֵ��
��3����![]() Ϊ��ֵʱ����������������ʱ�������ﵽ��������Ϊ����
Ϊ��ֵʱ����������������ʱ�������ﵽ��������Ϊ����![]() ��
��
���𰸡���1��![]() �ף���2��15����3����
�ף���2��15����3����![]() Ϊ12ʱ����������������������Ϊ
Ϊ12ʱ����������������������Ϊ![]() ��
��
��������
��1�����������ͼ�Σ������ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��![]() �ij���
�ij���
��2�����ݳ����ε�������㹫ʽ���Եõ���Ӧ�ķ��̣��Ӷ����Եõ�![]() ��ֵ��ע��ǽ�����ó���Ϊ27�ף�
��ֵ��ע��ǽ�����ó���Ϊ27�ף�
��3������������Եõ�![]() ��
��![]() �ĺ�����ϵʽ��Ȼ����ݶ��κ��������ʺ�
�ĺ�����ϵʽ��Ȼ����ݶ��κ��������ʺ�![]() ��ȡֵ��Χ����ɣ�
��ȡֵ��Χ����ɣ�
�⣺��1����ͼ�ɵã�![]() �ij���
�ij���![]() ����
����![]() ��
��
��![]() �ij���
�ij���![]() �ף�
�ף�
��2����![]() ����ã�
����ã�![]() ��
��![]() ��
��
![]() ����
����![]() ��
��![]() ��
��
��![]() ��ֵ��15��
��ֵ��15��
��3�����������������![]() ����
����![]() ��
��
![]() ����
����![]() ��
��
![]() ��
��![]() ʱ��
ʱ��![]() ȡ�����ֵ����ʱ
ȡ�����ֵ����ʱ![]() ��
��
�𣺵�![]() Ϊ12ʱ����������������ʱ�������ﵽ��������Ϊ
Ϊ12ʱ����������������ʱ�������ﵽ��������Ϊ![]() ��
��


 ȫ��������ϵ�д�
ȫ��������ϵ�д� һ��һ����ʱ���ϵ�д�
һ��һ����ʱ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�У���ABC��90��������ABC�Ƶ�B��ʱ����ת90����A�Ķ�Ӧ��Ϊ��D����C�Ķ�Ӧ��Ϊ��E��ֱ��DE��ֱ��AC���ڵ�F������FB��
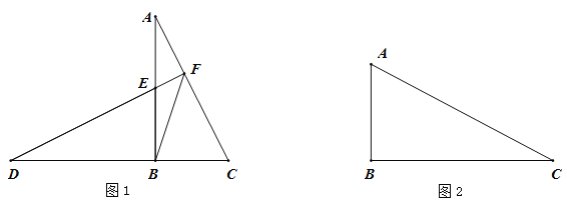
��1����ͼ1������BAC��45��ʱ��
����֤��DF��AC��
�����DFB�Ķ�����
��2����ͼ2������BAC��45��ʱ��
���������ⲹȫͼ2��
���õ�ʽ��ʾ�߶�FC��FB��FE֮���������ϵ����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
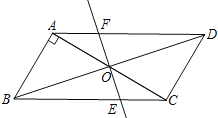
����Ŀ����֪����ͼ��ƽ���ı���ABCD�У�AB��AC��AB=1,BC=![]() ���Խ���AC��BD����O�㣬��ֱ��AC�Ƶ�O˳ʱ����ת���ֱ�BC��AD�ڵ�E��F��
���Խ���AC��BD����O�㣬��ֱ��AC�Ƶ�O˳ʱ����ת���ֱ�BC��AD�ڵ�E��F��
��1����֤������ת��Ϊ90��ʱ���ı���ABEF��ƽ���ı��Σ�
��2������ת�����У��ı���BEDF������������������ܣ���˵�����ɣ����ܣ�˵�����ɲ������ʱAC�Ƶ�O˳ʱ����ת�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ�� ![]() �DZ߳�Ϊ3cm�ĵȱ������Σ�����P��Qͬʱ��A��B����������ֱ���AB��BC���������ƶ������ǵ��ٶȶ���
�DZ߳�Ϊ3cm�ĵȱ������Σ�����P��Qͬʱ��A��B����������ֱ���AB��BC���������ƶ������ǵ��ٶȶ���![]() ������P�����Bʱ��P��Q����ֹͣ�˶������P���˶�ʱ��
������P�����Bʱ��P��Q����ֹͣ�˶������P���˶�ʱ��![]() ��������и����⣺
��������и����⣺
![]() ����
����![]() ��ʱ����
��ʱ����![]() �������
�������
![]() ��tΪ��ֵʱ��
��tΪ��ֵʱ�� ![]() ��ֱ�������Σ�
��ֱ�������Σ�
![]() �Ƿ����ijһʱ��t��ʹ�ı���APQC�������
�Ƿ����ijһʱ��t��ʹ�ı���APQC�������![]() ���������֮����������ڣ����t��ֵ����������˵�����ɣ�
���������֮����������ڣ����t��ֵ����������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
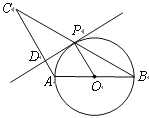
����Ŀ����֪����ͼ��![]() �У�
��![]() ����
����![]() Ϊֱ������O��
Ϊֱ������O��![]() �ڵ�
�ڵ�![]() ��
��
![]() �ڵ�
�ڵ�![]() ��
��
��1����֤��![]() ����O�����ߣ�
����O�����ߣ�
��2����![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪Rt��ABC�У���C = 90����AD�ǡ�BAC�Ľ�ƽ���ߣ�
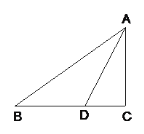
(1)��߹���ͼ������O��ʹԲ��O��AB�ϣ���A����Բ��O�ϣ�![]() (��д������������ͼ�ۼ�)��
(��д������������ͼ�ۼ�)��
(2)�ж�ֱ��BC��������O��λ�ù�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
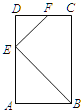
����Ŀ����ͼ���ھ���ABCD�У�AB=6��AD=12����E��AD���ϣ���AE=8��EF��BE��CD�ڵ�F.
��1����֤����ABE�ס�DEF��
��2����CF�ij�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����λͬѧ5����ѧѡ�����ijɼ�ͳ�����±�������5�ο��Ե��ܳɼ���ͬ����ͬѧ������������⣺
��1 �� | ��2 �� | �� 3�� | �� 4�� | ��5 �� | |
�׳ɼ� | 90 | 40 | 70 | 40 | 60 |
�ҳɼ� | 70 | 50 | 70 |
| 70 |
��1��ͳ�Ʊ��У���![]() ��ֵ����ͬѧ�ɼ��ļ���Ϊ���٣�
��ֵ����ͬѧ�ɼ��ļ���Ϊ���٣�
��2��Сӱ�����˼�ͬѧ�ijɼ�ƽ����Ϊ60��������![]() [(90��60)2+(40��60)2+(70��60)2+(40��60)2+(60��60)2]��360.
[(90��60)2+(40��60)2+(70��60)2+(40��60)2+(60��60)2]��360.
���������ͬѧ�ɼ���ƽ�����ͷ��
��3����ƽ�����ͷ���ĽǶȷ�����������λͬѧ˭�ijɼ����ȶ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������֪����
���е�����ֵ������ֱ��ƽ�еģ���ˣ�����������ֱ�����ߵ���Ŀ�ĵأ�ֻ�ܰ�ֱ�ǹ���ķ�ʽ���ߣ������սֵ��Ĵ�ֱ��ƽ�з�����ƽ��ֱ������ϵxOy��������A(![]() ��
��![]() )��B(
)��B(![]() ��
��![]() )�������·�ʽ�����������룺d(A��B)��
)�������·�ʽ�����������룺d(A��B)��![]() ��
��![]() ��
��
����ѧ���⣩��
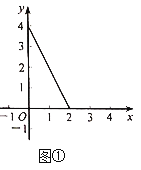
��1������֪��A(��2��1)����d(O��A)�� ���ں���![]() (0��x��2)��ͼ����ͼ����ʾ��B��ͼ����һ�㣬d(O��B)��3�����B�������� ��
(0��x��2)��ͼ����ͼ����ʾ��B��ͼ����һ�㣬d(O��B)��3�����B�������� ��
��2������![]() (x��0)��ͼ����ͼ����ʾ����֤���ú�����ͼ���ϲ����ڵ�C��ʹd(O��C)��3��
(x��0)��ͼ����ͼ����ʾ����֤���ú�����ͼ���ϲ����ڵ�C��ʹd(O��C)��3��

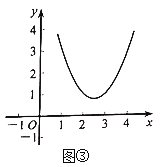
��3������![]() (x��0)��ͼ����ͼ����ʾ��D��ͼ����һ�㣬��d(O��D)����Сֵ����Ӧ�ĵ�D�����꣮
(x��0)��ͼ����ͼ����ʾ��D��ͼ����һ�㣬��d(O��D)����Сֵ����Ӧ�ĵ�D�����꣮
������������
��4��ij��Ҫ��һ��ͨ�����ۺ��ĵ�·����ͼ�ܣ���·��MΪ��㣬����MN����ij�������ڸô���һ��ֱ������ֱ�ߵ����ߣ��������ʹ��·��̣���Ҫ�����ʵ���ƽ��ֱ������ϵ������ʾ��ͼ����Ҫ˵�����ɣ�
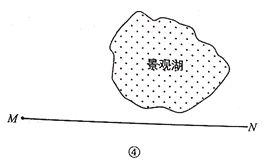
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com