【题目】已知：如图，
中，
，以
为直径的⊙O交
于点
，
于点
．
（1）求证：
是⊙O的切线；
（2）若
，求的值．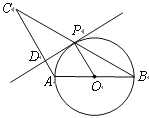
【答案】（1）见解析；（2）
【解析】
试题（1）由OB=OP可得∠B=∠OPB，由
可得∠B=∠C，即可证得OP∥AC，再结合
即可证得结论；
(2)连接AP，根据直径所对是圆周角是直角可得AP⊥BC，再根据等腰三角形的三线合一的性质可得BP=CP，最后利用含30°角的直角三角形的性质结合勾股定理即可求得结果。
（1）∵OB=OP
∴∠B=∠OPB
∵
∴∠B=∠C
∴∠C=∠OPB
∴OP∥AC
∴∠OPD=∠CDP=90°
∵OP是半径
∴
是⊙O的切线；
(2)连接AP
∵AB是直径
∴AP⊥BC
∵
∴BP=CP，∠B=∠C
∵∠CAB=120°
∴∠B=∠C=30°
∴在Rt△ABP中，
在Rt△ABP中，
∴
.
科目：初中数学 来源： 题型：
【题目】已知二次函数y =x2 + 4x + 3．
（1）将二次函数的表达式化为y = a (x-h)2 + k 的形式；
（2）在平面直角坐标系xOy中，用描点法画出这个二次函数的图象；
x | … | … | |||||
y | … | … |
（3）观察图象，直接写出当
时
的取值范围；
（4）根据（2）中的图象，写出一条该二次函数的性质．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，小芳家的落地窗（线段DE）与公路（直线PQ）互相平行，她每天做完作业后都会在点A处向窗外的公路望去．
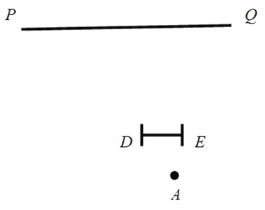
（1）请在图中画出小芳能看到的那段公路并记为BC．
（2）小芳很想知道点A与公路之间的距离，于是她想到了一个办法．她测出了邻家小彬在公路BC段上走过的时间为10秒，又测量了点A到窗的距离是4米，且窗DE的长为3米，若小彬步行的平均速度为1.2米/秒，请你帮助小芳计算出点A到公路的距离．
查看答案和解析>>
科目：初中数学 来源： 题型：
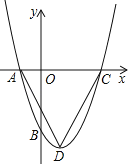
【题目】如图，抛物线y＝x2+bx+c与x轴交于A，C两点，与y轴交于B点，抛物线的顶点为点D，已知点A的坐标为(﹣1，0)，点B的坐标为(0，﹣3).
(1)求抛物线的解析式及顶点D的坐标.
(2)求△ACD的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
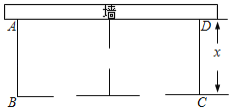
【题目】某农场要建一个饲养场（长方形
，饲养场的一面靠墙（墙最大可用长度为27米），另三边用木栏围成，中间也用木栏隔开，分成两个场地，并在如图所示的三处各留1米宽的门（不用木栏），建成后木栏总长60米，设饲养场（长方形的宽为
米．
（1）求饲养场的长
（用含的代数式表示）．
（2）若饲养场的面积为
，求的值．
（3）当为何值时，饲养场的面积最大，此时饲养场达到的最大面积为多少
？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：关于
的一元二次方程
（
是整数）．
(1)求证：方程有两个不相等的实数根；
(2)若方程的两个实数根分别为
，
（其中
），设
，则
是否为变量的函数？如果是，求出函数的解析式；如果不是，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为了解九年级学生的体育达标情况，随机抽取
名九年级学生进行体育达标项目测试，测试成绩如下表，请根据表中的信息，解答下列问题：
测试成绩（分） |
|
|
|
|
|
人数（人） |
|
|
|
|
|
（1）该校九年级有
名学生，估计体育测试成绩为
分的学生人数；
（2）该校体育老师要对本次抽测成绩为
分的甲、乙、丙、丁
名学生进行分组强化训练，要求两人一组，求甲和乙恰好分在同一组的概率．（用列表或树状图方法解答）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一次数学活动课中，某数学小组探究求环形花坛（如图所示）面积的方法，现有以下工具；①卷尺；②直棒EF；③T型尺（CD所在的直线垂直平分线段AB）．
（1）在图1中，请你画出用T形尺找大圆圆心的示意图（保留画图痕迹，不写画法）；
（2）如图2，小华说：“我只用一根直棒和一个卷尺就可以求出环形花坛的面积，具体做法如下：
将直棒放置到与小圆相切，用卷尺量出此时直棒与大圆两交点M，N之间的距离，就可求出环形花坛的面积”如果测得MN=10m，请你求出这个环形花坛的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
