
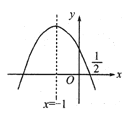
【题目】如图,抛物线![]() 的对称轴是
的对称轴是![]() ,且过点(
,且过点(![]() ,0),有下列结论:①
,0),有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ;其中正确的结论个数为( )
;其中正确的结论个数为( )
A.1B.2C.3D.4
【答案】C
【解析】
根据抛物线的开口方向、对称轴、与y轴的交点判定系数符号,运用一些特殊点和抛物线的最值判定表达式的符号.
由抛物线的开口向下可得:a<0,因为抛物线的对称轴在y轴左边可得:a,b同号,所以b<0,根据抛物线与y轴的交点在正半轴可得:c>0,∴abc>0,故①正确;
∵直线x=﹣1是抛物线y=ax2+bx+c(a≠0)的对称轴,∴![]() 1,∴b=2a,a﹣2b+4c=a﹣4a+4c=﹣3a+4c.
1,∴b=2a,a﹣2b+4c=a﹣4a+4c=﹣3a+4c.
∵a<0,∴﹣3a>0,∴﹣3a+4c>0,即a﹣2b+4c>0,故②错误;
∵抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(![]() ,0),∴抛物线与x轴的另一个交点坐标为(
,0),∴抛物线与x轴的另一个交点坐标为(![]() ,0),当x
,0),当x![]() 时,y=0,即a(
时,y=0,即a(![]() )2
)2![]() b+c=0,整理得:25a﹣10b+4c=0,故③正确;
b+c=0,整理得:25a﹣10b+4c=0,故③正确;
∵b=2a,a+b+c<0,∴![]() b+b+c=0,即3b+2c<0,故④错误;
b+b+c=0,即3b+2c<0,故④错误;
∵x=﹣1时,函数值最大,∴a﹣b+c≥m2a﹣mb+c,∴a﹣b≥m(am﹣b),所以⑤正确.
故选B.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
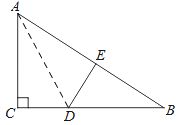
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为6,E,F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.

(1)求证:EF=MF;
(2)若AE=2,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
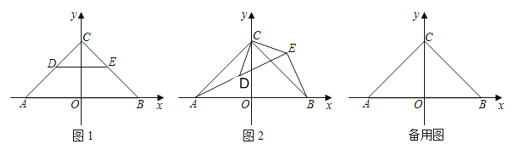
【题目】如图1,在平面直角坐标系中,点A(﹣![]() ,0),B(
,0),B(![]() ,0),C(0,
,0),C(0,![]() ).D,E分别是线段AC和CB上的点,CD=CE.将△CDE绕点C逆时针旋转一个角度α.
).D,E分别是线段AC和CB上的点,CD=CE.将△CDE绕点C逆时针旋转一个角度α.
(1)若0°<α<90°,在旋转过程中当点A,D,E在同一直线上时,连接AD,BE,如图2.求证:AD=BE,且AD⊥BE
(2)若0°<α<360°,D,E恰好是线段AC和CB上的中点,在旋转过程中,当DE∥AC时,求α的值及点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+mx+m﹣3=0.
(1)若该方程的一个根为2,求m的值及方程的另一个根;
(2)求证:不论m取何实数,该方程都有两个不相等的实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,6月7日为端午节.在端午节前夕,三位同学到某超市调研一种进价为2元的粽子的销售情况.请根据小丽提供的信息,解答小华和小明提出的问题.
小丽 | 每个定价3元,每天能卖出500个.若这种粽子的售价每上涨0.1元,其销售量将减少10个 |
小华 | 照你说,若要实现每天800元的销售利润,那该如何定价?别忘了,根据物价局规定,售价不能超过进价的 |
小明 | 若按照物价局规定的最高售价,每天的利润会超过800元吗?请判断并说明理由 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船c的求救信号.已知A、B两船相距100(![]() +3)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
+3)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
(1)分别求出A与C,A与D之间的距离AC和AD(如果运算结果有根号,请保留根号).
(2)已知距观测点D处200海里范围内有暗礁.若巡逻船A沿直线AC去营救船C,在去营救的途中有无触暗礁危险?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过两点A(﹣3,0),B(0,3),且其对称轴为直线x=﹣1.
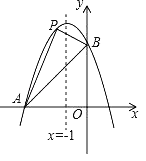
(1)求此抛物线的解析式.
(2)若点Q是对称轴上一动点,当OQ+BQ最小时,求点Q的坐标.
(3)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求△PAB面积的最大值,并求出此时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com