
【题目】如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船c的求救信号.已知A、B两船相距100(![]() +3)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
+3)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
(1)分别求出A与C,A与D之间的距离AC和AD(如果运算结果有根号,请保留根号).
(2)已知距观测点D处200海里范围内有暗礁.若巡逻船A沿直线AC去营救船C,在去营救的途中有无触暗礁危险?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

【答案】(1)A与C之间的距离AC为200![]() 海里,A与D之间的距离AD为200(3﹣
海里,A与D之间的距离AD为200(3﹣![]() )海里;(2)巡逻船A沿直线AC去营救船C,在去营救的途中无触暗礁危险.
)海里;(2)巡逻船A沿直线AC去营救船C,在去营救的途中无触暗礁危险.
【解析】
(1)作CE⊥AB于点E,则∠ABC=45°,∠BAC=60°,设AE=x海里,在Rt△AEC中,CE=AEtan60°,在Rt△BCE中,BE=CE=![]() x,由AE+BE=x+
x,由AE+BE=x+![]() x=100(3+
x=100(3+![]() )求出x的值,再根据AC=2x得出AC的值,在△ACD中,由∠DAC=60°,∠ADC=75°得出∠ACD=45°.过点D作DF⊥AC于点F,设AF=y,则DF=CF=
)求出x的值,再根据AC=2x得出AC的值,在△ACD中,由∠DAC=60°,∠ADC=75°得出∠ACD=45°.过点D作DF⊥AC于点F,设AF=y,则DF=CF=![]() y,根据AC=y+
y,根据AC=y+![]() y=200
y=200![]() 求出y的值,故可得出AD的长,进而得出结论;
求出y的值,故可得出AD的长,进而得出结论;
(2)根据(1)中的结论得出DF的长,再与200相比较即可.
(1)作CE⊥AB于点E,则∠ABC=45°,∠BAC=60°,设AE=x海里,
∵在Rt△AEC中,CE=AEtan60°=![]() x,
x,
在Rt△BCE中,BE=CE=![]() x,
x,
∴AE+BE=x+![]() x=100(3+
x=100(3+![]() ),解得x=100
),解得x=100![]() ,
,
∴AC=2x=200![]() ,
,
在△ACD中,
∵∠DAC=60°,∠ADC=75°,
∴∠ACD=45°.
过点D作DF⊥AC于点F,设AF=y,则DF=CF=![]() y,
y,
∴AC=y+![]() y=200
y=200![]() ,解得y=100(3﹣
,解得y=100(3﹣![]() ),
),
∴AD=2y=200(3﹣![]() ).
).
答:A与C之间的距离AC为200![]() 海里,A与D之间的距离AD为200(3﹣
海里,A与D之间的距离AD为200(3﹣![]() )海里;
)海里;
(2)∵由(1)可知,DF=![]() AF=
AF=![]() ×100(3﹣
×100(3﹣![]() )≈219,
)≈219,
∵219>200,
∴巡逻船A沿直线AC去营救船C,在去营救的途中无触暗礁危险.


科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+b与反比例函数y=![]() 的图形交于A(a,4)和B(4,1)两点.
的图形交于A(a,4)和B(4,1)两点.
(1)求b,k的值;
(2)在第一象限内,当一次函数y=﹣x+b的值大于反比例函数y=![]() 的值时,直接写出自变量x的取值范围;
的值时,直接写出自变量x的取值范围;
(3)将直线y=﹣x+b向下平移m个单位,当直线与双曲线只有一个交点时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自我省深化课程改革以来,某校开设了:A.利用影长求物体高度,B.制作视力表,C.设计遮阳棚,D.制作中心对称图形,四类数学实践活动课.规定每名学生必选且只能选修一类实践活动课,学校对学生选修实践活动课的情况进行抽样调查,将调查结果绘制成如下两幅不完整的统计图.
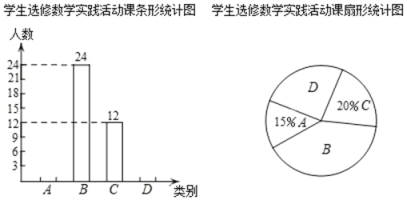
根据图中信息解决下列问题:
(1)本次共调查名学生,扇形统计图中B所对应的扇形的圆心角为度;
(2)补全条形统计图;
(3)选修D类数学实践活动的学生中有2名女生和2名男生表现出色,现从4人中随机抽取2人做校报设计,请用列表或画树状图法求所抽取的两人恰好是1名女生和1名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):根据以上信息解答下列问题:
(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图.
(3)若该中学约有800名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?并根据以上调查结果,就中学生如何合理使用手机给出你的一条建议.
选项 | 频数 | 频率 |
A | 10 | m |
B | n | 0.2 |
C | 5 | 0.1 |
D | p | 0.4 |
E | 5 | 0.1 |
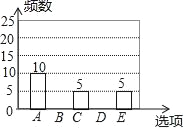
查看答案和解析>>
科目:初中数学 来源: 题型:
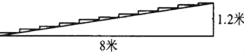
【题目】每年的5月15日是”世界助残日”,某商场门前的台阶共高出地面1.2米,为帮助残疾人,便于轮椅行走,准备拆除台阶换成斜坡,又考虑安全,轮椅行走斜坡的坡角不得超过9°,已知此商场门前的人行道距门前垂直距离为8米(斜坡不能修在人行道上),问此商场能否把台阶换成斜坡?(参考数据sin9°=0.1564,cos9°=0.9877,tan9°=0.1584)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成任务:
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中,错误的是( )
A. 抛物线于x轴的一个交点坐标为(﹣2,0)
B. 抛物线与y轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y1=x2+mx+n的图象经过点P(﹣3,1),对称轴是经过(﹣1,0)且平行于y轴的直线.
(1)求m,n的值.
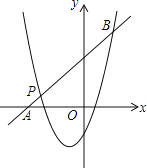
(2)如图,一次函数y2=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA:PB=1:5,求一次函数的表达式.
(3)直接写出y1>y2时x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com