
����Ŀ����ͼ��С���ҵ���ش����߶�DE���빫·��ֱ��PQ������ƽ�У���ÿ��������ҵ���ڵ�A������Ĺ�·��ȥ��
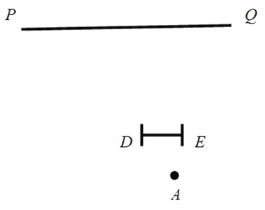
��1������ͼ�л���С���ܿ������Ƕι�·����ΪBC��
��2��С������֪����A�빫·֮��ľ��룬�������뵽��һ���취����������ڼ�С���ڹ�·BC�����߹���ʱ��Ϊ10�룬�ֲ����˵�A�����ľ�����4�ף��Ҵ�DE�ij�Ϊ3�ף���С���е�ƽ���ٶ�Ϊ1.2��/�룬�������С���������A����·�ľ��룮
���𰸡�(1)������;(2)16m
��������
��1������AD��AE���ӳ�����PQ��B��C����BC��Ϊ����
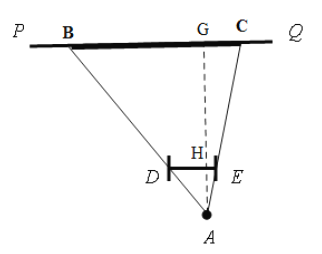
��2����A��AG��PQ��G����DE��H���ɴ�DE��·PQƽ�У��ɵ���ADE�ס�ABC�������õ�![]() ��BC�ij��ȿɸ���С����ٶȺ�ʱ�������AH��DE��֪���ݴ˿����AG.
��BC�ij��ȿɸ���С����ٶȺ�ʱ�������AH��DE��֪���ݴ˿����AG.
�⣺��1����ͼ��BC��Ϊ����
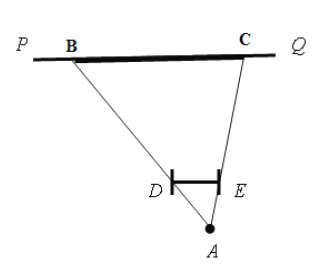
��2����A��AG��PQ��G����DE��H��
�������֪��DE //BC��DE=3��AH=4��![]() ��
��
��![]() ��
��
��![]() ����
����![]() ��
��
��AG=16��
�𣺵�A����·�ľ�����16m.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
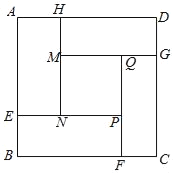
����Ŀ���������˵Ķ�Ա����3D��ӡ���һ���߳�Ϊ6����������ƷABCD�����ͼ����ͼ��ʾ��������Ӱ���ĸ�ȫ�ȵľ��Σ��ò��ϼ״�ӡ����������������MNPQ���ò����Ҵ�ӡ�����ڴ�ӡ��ȱ�����ͬ������£����ֲ��ϵ����ijɱ����±���
���� | �� | �� |
�۸�Ԫ/��2�� | 80 | 50 |
����εĽ϶̱�AH�ij�Ϊx�ף���ӡ���ϵ��ܷ���ΪyԪ��
��1��MQ�ij�Ϊ�� ���ף��ú�x�Ĵ���ʽ��ʾ����
��2����y����x�ĺ�������ʽ��
��3�����������ı߳���С��2��ʱ��Ԥ�����ϵĹ����ʽ�2800Ԫ�����������ú�������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]()
(1)���仯��![]() ����ʽ_______________��
����ʽ_______________��
(2)��������_________�Գ��᷽��_______________��
(3)����㷨�������κ�����ͼ��
(4) ��![]() ʱ��д��
ʱ��д��![]() ��ȡֵ��Χ
��ȡֵ��Χ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ�һԪ���η���![]() ����
����![]() ʱ��������Ϊ
ʱ��������Ϊ![]() ��
��![]() ����������ϵ���Ĺ�ϵΪ��
����������ϵ���Ĺ�ϵΪ��![]() ��
��![]() .
.
Ӧ�ã�
��1������![]() ����ʵ�����ֱ�Ϊ
����ʵ�����ֱ�Ϊ![]() ��
��![]() ����
����![]() ______��
______��![]() _____��
_____��
��2��������![]() �ķ���
�ķ���![]() ��������ʵ����
��������ʵ����![]() ��
��![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3���ڣ�2���������£�������![]() ����ʵ��
����ʵ��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�ı߳�Ϊ6��E��F�ֱ���AB��BC���ϵĵ㣬�ҡ�EDF=45��������DAE�Ƶ�D��ʱ����ת90�����õ���DCM��

(1)��֤��EF=MF��
(2)��AE=2����FC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
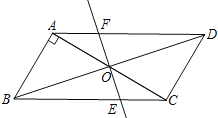
����Ŀ����֪����ͼ��ƽ���ı���ABCD�У�AB��AC��AB=1,BC=![]() ���Խ���AC��BD����O�㣬��ֱ��AC�Ƶ�O˳ʱ����ת���ֱ�BC��AD�ڵ�E��F��
���Խ���AC��BD����O�㣬��ֱ��AC�Ƶ�O˳ʱ����ת���ֱ�BC��AD�ڵ�E��F��
��1����֤������ת��Ϊ90��ʱ���ı���ABEF��ƽ���ı��Σ�
��2������ת�����У��ı���BEDF������������������ܣ���˵�����ɣ����ܣ�˵�����ɲ������ʱAC�Ƶ�O˳ʱ����ת�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
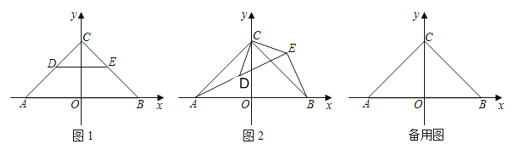
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���A(��![]() ��0)��B(
��0)��B(![]() ��0)��C(0��
��0)��C(0��![]() ).D��E�ֱ����߶�AC��CB�ϵĵ㣬CD��CE.����CDE�Ƶ�C��ʱ����תһ���Ƕ���.
).D��E�ֱ����߶�AC��CB�ϵĵ㣬CD��CE.����CDE�Ƶ�C��ʱ����תһ���Ƕ���.
(1)��0��������90��������ת�����е���A��D��E��ͬһֱ����ʱ������AD��BE����ͼ2.��֤��AD��BE����AD��BE
(2)��0��������360����D��Eǡ�����߶�AC��CB�ϵ��е㣬����ת�����У���DE��ACʱ��������ֵ����E������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
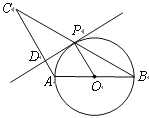
����Ŀ����֪����ͼ��![]() �У�
��![]() ����
����![]() Ϊֱ������O��
Ϊֱ������O��![]() �ڵ�
�ڵ�![]() ��
��
![]() �ڵ�
�ڵ�![]() ��
��
��1����֤��![]() ����O�����ߣ�
����O�����ߣ�
��2����![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���ʺϲ�ͬ��Ⱥ�Ŀ�ζ��ij�̵��ƻ��ζ����ݮζ��ţ��ζ���ǹ������װ�ɼס������ִ�װ��������.����ÿ��װ��ƻ��ζ����ݮζ��ţ��ζ���ǹ���10�ţ�����ÿ��װ��ƻ��ζ�ǹ�20�ţ���ݮζ��ţ��ζ�ǹ���5��.�ס������ִ�װ�ǹ�ÿ���ɱ��۷ֱ��Ǵ��и����ǹ��ɱ�֮��.��֪ÿ��ƻ��ζ���ǹ��ɱ���Ϊ0.4Ԫ�����ִ�װ�ǹ����ۼ�Ϊ23.4Ԫ��������Ϊ30%�����ִ�װ�ǹ�ÿ����������Ϊ20%.�������ִ�װ�����������ʴﵽ24%����ù�˾���ۼס������ִ�װ�ǹ�������֮����__________.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com