
【题目】(概念认知):
城市的许多街道是相互垂直或平行的,因此,往往不能沿直线行走到达目的地,只能按直角拐弯的方式行走.可以按照街道的垂直和平行方向建立平面直角坐标系xOy,对两点A(![]() ,
,![]() )和B(
)和B(![]() ,
,![]() ),用以下方式定义两点间距离:d(A,B)=
),用以下方式定义两点间距离:d(A,B)=![]() +
+![]() .
.
(数学理解):
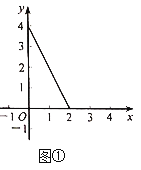
(1)①已知点A(﹣2,1),则d(O,A)= ;②函数![]() (0≤x≤2)的图像如图①所示,B是图像上一点,d(O,B)=3,则点B的坐标是 .
(0≤x≤2)的图像如图①所示,B是图像上一点,d(O,B)=3,则点B的坐标是 .
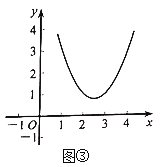
(2)函数![]() (x>0)的图像如图②所示,求证:该函数的图像上不存在点C,使d(O,C)=3.
(x>0)的图像如图②所示,求证:该函数的图像上不存在点C,使d(O,C)=3.

(3)函数![]() (x≥0)的图像如图③所示,D是图像上一点,求d(O,D)的最小值及对应的点D的坐标.
(x≥0)的图像如图③所示,D是图像上一点,求d(O,D)的最小值及对应的点D的坐标.
(问题解决):
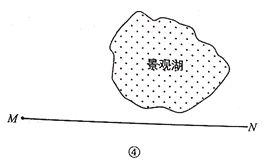
(4)某市要修建一条通往景观湖的道路,如图④,道路以M为起点,先沿MN方向到某处,再在该处拐一次直角弯沿直线到湖边,如何修建能使道路最短?(要求:建立适当的平面直角坐标系,画出示意图并简要说明理由)
【答案】(1)【数学理解】:① 3, ② (1,2) ;(2)见解析;(3)![]() 有最小值3,此时点
有最小值3,此时点![]() 的坐标是(2,1);【问题解决】:(4)先沿
的坐标是(2,1);【问题解决】:(4)先沿![]() 方向修建到
方向修建到![]() 处,再沿
处,再沿![]() 方向修建到
方向修建到![]() 处,见解析.
处,见解析.
【解析】
(1)①根据定义可求出d(O,A)=|0+2|+|01|=2+1=3;②由两点间距离:d(A,B)=|x1x2|+|y1y2|及点B是函数y=2x+4的图象上的一点,可得出方程组,解方程组即可求出点B的坐标;
(2)由条件知x>0,根据题意得![]() ,整理得x23x+4=0,由△<0可证得该函数的图象上不存在点C,使d(O,C)=3.
,整理得x23x+4=0,由△<0可证得该函数的图象上不存在点C,使d(O,C)=3.
(3)根据条件可得|x|+|x25x+7|,去绝对值后由二次函数的性质可求出最小值;
(4)以M为原点,MN所在的直线为x轴建立平面直角坐标系xOy,将函数y=x的图象沿y轴正方向平移,直到与景观湖边界所在曲线有交点时停止,设交点为E,过点E作EH⊥MN,垂足为H,修建方案是:先沿MN方向修建到H处,再沿HE方向修建到E处,可由d(O,P)≥d(O,E)证明结论即可.
解:(1)①由题意得:d(O,A)=|0+2|+|01|=2+1=3;
②设B(x,y),由定义两点间的距离可得:|0x|+|0y|=3,
∵0≤x≤2,
∴x+y=3,
∴![]() ,
,
解得: x=1,y=2,
∴B(1,2),
(2)假设函数![]() 的图像上存在点
的图像上存在点![]() ,使
,使![]() .
.
根据题意,得![]() .
.
因为![]() ,所以
,所以![]() .
.
所以![]() .
.
方程两边乘![]() ,得
,得![]() .
.
整理,得![]() .
.
因为![]() ,
,
所以方程![]() 无实数根.
无实数根.
所以函数![]() 的图像上不存在点
的图像上不存在点![]() ,使
,使![]() .
.
(3)设![]() .
.
根据题意,得![]() .
.
因为![]() ,又
,又![]() ,
,
所以![]() .
.
所以当![]() 时,
时,![]() 有最小值3,此时点
有最小值3,此时点![]() 的坐标是
的坐标是![]() .
.
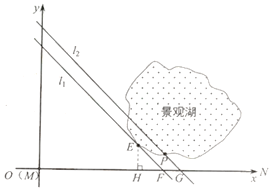
(4)如图,以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴建立平面直角坐标系
轴建立平面直角坐标系![]() .将函数
.将函数![]() 的图像沿
的图像沿![]() 轴正方向平移.直到与景观湖边界所在曲线有交点时停止.设交点为
轴正方向平移.直到与景观湖边界所在曲线有交点时停止.设交点为![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() .修建方案是:先沿
.修建方案是:先沿![]() 方向修建到
方向修建到![]() 处,再沿
处,再沿![]() 方向修建到
方向修建到![]() 处.
处.
理由:设过点![]() 的直线
的直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .在景观湖边界所在曲线上任取一点
.在景观湖边界所在曲线上任取一点![]() ,过点
,过点![]() 作直线
作直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .因为
.因为![]() ,所以
,所以![]() .同理
.同理![]() .因为
.因为![]() ,所以
,所以![]() .因此,上述方案修建的道路最短.
.因此,上述方案修建的道路最短.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
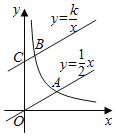
【题目】如图,直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0,x>0)交于点A,将直线y=
(k>0,x>0)交于点A,将直线y=![]() x向上平移2个单位长度后,与y轴交于点C,与双曲线交于点B,若OA=3BC,则k的值为____.
x向上平移2个单位长度后,与y轴交于点C,与双曲线交于点B,若OA=3BC,则k的值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=4![]() ,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为______.
,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
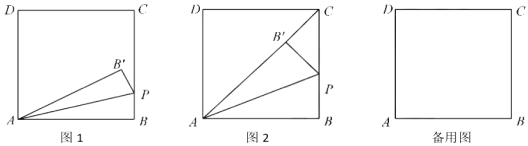
【题目】如图1,在矩形![]() 中,BC=3,动点
中,BC=3,动点![]() 从
从![]() 出发,以每秒1个单位的速度,沿射线
出发,以每秒1个单位的速度,沿射线![]() 方向移动,作
方向移动,作![]() 关于直线
关于直线![]() 的对称
的对称![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]()
(1)若![]()
①如图2,当点B’落在AC上时,显然△PCB’是直角三角形,求此时t的值
②是否存在异于图2的时刻,使得△PCB’是直角三角形?若存在,请直接写出所有符合题意的t的值?若不存在,请说明理由
(2)当P点不与C点重合时,若直线PB’与直线CD相交于点M,且当t<3时存在某一时刻有结论∠PAM=45°成立,试探究:对于t>3的任意时刻,结论∠PAM=45°是否总是成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
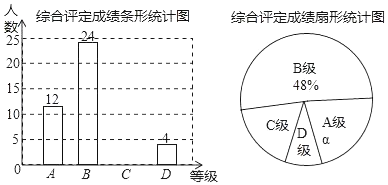
【题目】设中学生体质健康综合评定成绩为x分,满分为100分,规定:85≤x≤100为A级,75≤x≤85为B级,60≤x≤75为C级,x<60为D级.现随机抽取某中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图,请根据图中的信息,解答下列问题:
(1)在这次调查中,一共抽取了 名学生,α= %;
(2)补全条形统计图;
(3)扇形统计图中C级对应的圆心角为 度;
(4)若A级由2个男生参加自主考试,B级由1个女生参加自主考试,刚好有一男一女考取名校,请用树状图或列表法求他们的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与思考:
阿基米德(公元前287年一公元前212年),伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家,静态力学和流体静力学的奠基人,阿基米德流传于世的著作有10余种,多为希腊文手稿下面是《阿基米德全集》中记载的一个命题:AB是⊙O的弦,点C在⊙O上,且CD⊥AB于点D,在弦AB上取点E,使AD=DE,点F是![]() 上的一点,且
上的一点,且![]() =
=![]() ,连接BF可得BF=BE.
,连接BF可得BF=BE.
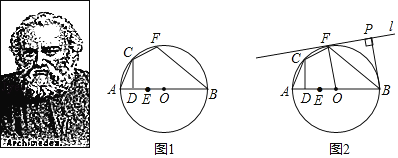
(1)将上述问题中弦AB改为直径AB,如图1所示,试证明BF=BE;
(2)如图2所示,若直径AB=10,EO=![]() OB,作直线l与⊙O相切于点F.过点B作BP⊥l于点P.求BP的长.
OB,作直线l与⊙O相切于点F.过点B作BP⊥l于点P.求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
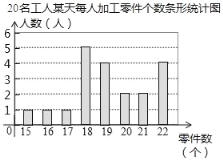
【题目】某部门为了解工人的生产能力情况,进行了抽样调查.该部门随机抽取了20名工人某天每人加工零件的个数,数据如下:整理上面数据,得到条形统计图;样本数据的平均数、众数、中位数如表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 19.2 | m | n |
根据以上信息,解答下列问题:
(1)上表中m、n的值分别为 , ;
(2)为调动积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让60%左右的工人能获奖,应根据 来确定奖励标准比较合适(填“平均数”、“众数”或“中位数”);
(3)该部门规定:每天加工零件的个数达到或超过21个的工人为生产能手若该部门有300名工人,试估计该部门生产能手的人数;
(4)现决定从小王、小张、小李、小刘中选两人参加业务能手比赛,直接写出恰好选中小张、小李两人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
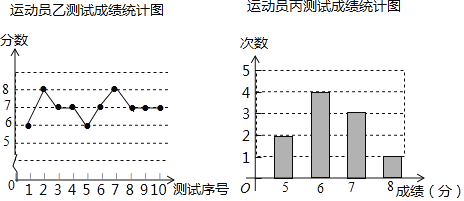
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么? (参考数据:三人成绩的方差分别为![]() 、
、![]() 、
、![]() )
)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com