
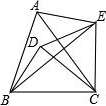
 如图,△ABC和△EDC都是等边三角形,连接BD、AE、BE,∠DBE=20°,则∠AEB=( )
如图,△ABC和△EDC都是等边三角形,连接BD、AE、BE,∠DBE=20°,则∠AEB=( )| A. | 30 | B. | 40 | C. | 45 | D. | 60 |
分析 先证△BCD≌ACE,得出∠CBD=∠CAE,再利△ABE内角和为180°建立角度等式,适当变形,将其它角度消去,得出∠AEB的度数.
解答 解:∵∠BCD+∠DCA=∠DCA+∠ACE=60°,
∴∠BCD=∠ACE,
在△BCD和△ACE中,
$\left\{\begin{array}{l}{DC=EC}\\{∠BCD=∠ACE}\\{BC=AC}\end{array}\right.$,
∴△BCD≌ACE(SAS),
∴∠CBD=∠CAE,
∵∠DBE=20°,
∠CBE=∠DBC-20°,
∵∠ABE+∠BEA+∠EAB=180°,
∴∠ABC-∠EBC+∠BEA+∠BAC+∠CAE=180°,
∴60°-(∠DBC-20°)+∠BEA+60°+∠CAE=180°,
∴60°-∠DBC+20°+∠BEA+60°+∠CAE=180°,
∴∠BEA=40°.
故选B.
点评 本题考查了等边三角形的性质、全等三角形的判定与性质、三角形内角和定理,难度适中.发现并证明△BCD≌ACE进而得出角相等是解决本题的突破口和关键.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将长方形纸片ABCD沿AE向上折叠,使点B落在DC边上的F点处,若△AFD的周长为9,△FCE的周长为3,则长方形ABCD的周长为12.
如图,将长方形纸片ABCD沿AE向上折叠,使点B落在DC边上的F点处,若△AFD的周长为9,△FCE的周长为3,则长方形ABCD的周长为12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
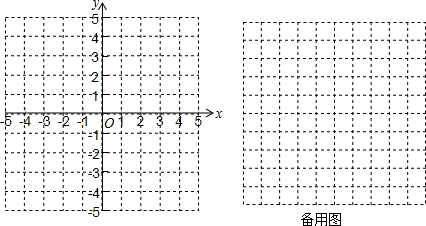
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
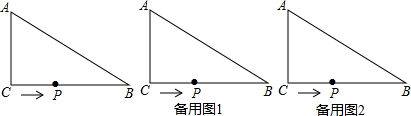
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
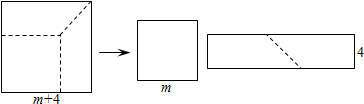
| A. | m+4 | B. | 2m+4 | C. | m+8 | D. | 2m-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com