
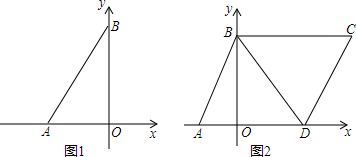
分析 (1)求出OB的长得出点C的坐标,求出AD的长即可求出点D的坐标,
(2)①分两种情况讨论:当P在AB上时,若⊙P与y轴相切,则1+0.5t=3-2t,当P在BD上时,若⊙P与y轴相切,则1+0.5t=2t-3,再求解即可,
②设⊙P的半径以acm/s的速度增加,当点P在菱形ABCD的对角线交点时,与四边形ABCD都相切,⊙P的半径1+$\frac{9}{4}$a,再求出BD和AC的交点坐标,最后根据若⊙P与四边形ABCD相切,则1+$\frac{9}{4}$a=1.5$\sqrt{3}$,即可得出答案,
(3)过O作OE⊥AB,根据△BOA∽△OEA,求出OE,从而求出S=$\frac{1}{2}$[(3$\sqrt{3}$)2π-(1.5$\sqrt{3}$)2π],再计算即可.
解答 解(1)∵OB=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
∴点C的坐标是(6,3$\sqrt{3}$),
∵AD=AB=6,
∴点D的坐标是(3,0),
(2)①当P在AB上时,若⊙P与y轴相切,则1+0.5t=3-2t,
t=$\frac{4}{5}$,
当P在BD上时,若⊙P与y轴相切,则1+0.5t=2t-3,
t=$\frac{8}{3}$,
②不存在
设⊙P的半径以acm/s的速度增加,
当点P在菱形ABCD的对角线交点时,到ABCD的距离相等,即与四边形ABCD都相切,
此时t=$\frac{9}{4}$,⊙P的半径1+$\frac{9}{4}$a,
设BD的解析式为:y=kx+b,AC的解析式为:y=ax+c,
解得:BD的解析式为:y=-$\sqrt{3}$x+3$\sqrt{3}$,AC的解析式为:y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$,
-$\sqrt{3}$x+3$\sqrt{3}$=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$,
解得;x=$\frac{3}{2}$,
则y=1.5$\sqrt{3}$,
若⊙P与四边形ABCD相切,
则1+$\frac{9}{4}$a=1.5$\sqrt{3}$,
解得:a=$\frac{6\sqrt{3}-4}{9}$,
则⊙P的半径以$\frac{6\sqrt{3}-4}{9}$cm/s的速度运动时就存在,
(3)过O作OE⊥AB,
则△BOA∽△OEA,
$\frac{BO}{OE}$=$\frac{BA}{OA}$,
解得;OE=1.5$\sqrt{3}$,
S=$\frac{1}{2}$[(3$\sqrt{3}$)2π-(1.5$\sqrt{3}$)2π]=$\frac{81}{8}$π,
则线段AB扫过的面积是$\frac{81}{8}$π.
点评 此题考查了圆的综合,用到的知识点是菱形的性质、切线的判定、相似三角形的判定与性质、一次函数,关键是作出辅助线构造相似三角形,注意分类讨论.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
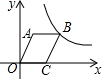 如图,在平行四边形OABC中,OC=3,OA=4,∠AOC=60°,若反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B,则k的值为10$\sqrt{3}$.
如图,在平行四边形OABC中,OC=3,OA=4,∠AOC=60°,若反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B,则k的值为10$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知锐角△ABC.
如图,已知锐角△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com